이 글은 경영학부 경영통계 수업에서 배운 자료들을 정리한 내용입니다.
Contents
-
두 모분산이 동일한지에 대한 가설검정을 위해 F 분포를 전용한다.
-
세 개 이상 모평균이 동일한지에 대한 가설검정을 위해 분산분석을 사용한다.
F분포
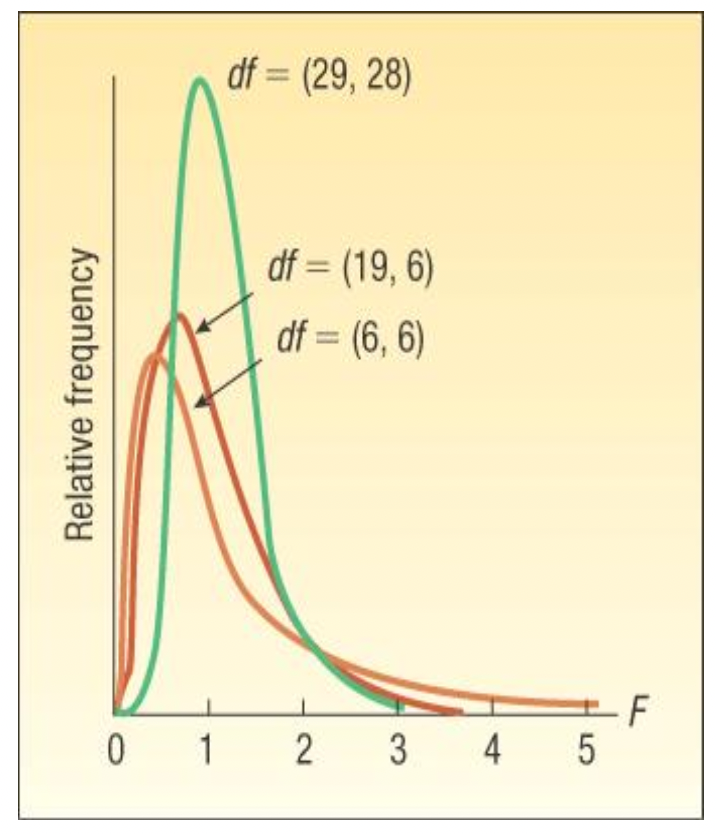
F-분포의 특성
-
F 분포는 t분포와 마찬가지로 다양함
-
연속적 (범위 : 0 ~ 무제한)
-
x축에 점근
-
F 값은 음수일 수가 없음 (최소값 = 0)
-
양의 비대칭정도를 가짐 (자유도 증가 → 정규분포와 유사해짐)
F-분포표
-
F값은 유의수준 $\alpha$ 와 두 자유도 v1, v2에 의해 결정됨
-
동일 모집단 분산의 비교 검정(= 검정통계량)
- $F = \frac{S_{1}^2}{S_{2}^2}$
분산분석
-
분산분석(ANOVA, Analysis of Variance) 특징
-
세계의 모평균을 비교할 때, z or t 검정을 할 경우 3번의 검정을 해야함
-
표본집단은 처리(Treatment)라 불림
-
분산분석은 인자(Factor)의 수에 따라 구분됨
-
-
검정통계량 : $F = \frac{MSB}{MSW}$ MSB: 처리간 제곱평균, MSW: 처리내 제곱평균
-
분산분석의 가정
-
정규성(Normality) : 모집단들은 서로 정규분포를 따른다. -
등분상성(Homoscedasticity) : 모집단들의 분산($\sigma$)은 동일하다. -
독립성(Independence) : 모집단들은 독립이다.
-
일원분산분석
-
변동을 표현하기위해 ANOVA에서는 제곱합(SS, Sum of Squares)을 사용
- SST(총 변동) = SSB(처리에 의한 변동) + SSW(처리와 관계 없는 임의 변동)
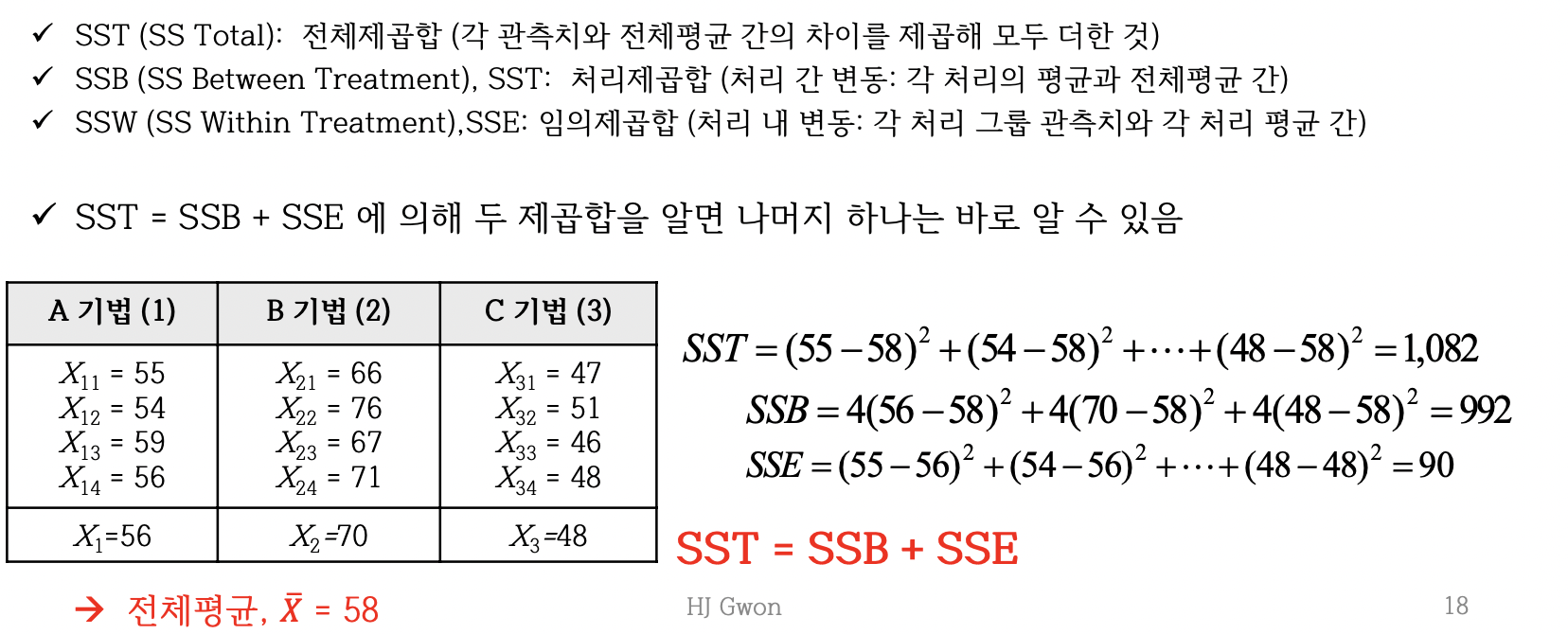
-
제곱평균(MS, Mean Squares (= SS/df = 제곱합/자유도))
-
F-검정을 위해 사용되는 두 분산
-
MSB: SSB의 제곱평균 (자유도: df = k - 1)
-
MSW(MSE): SSW(SSE)의 제곱평균 (자유도: df = n - k)
-
where k = 처리 그룹의 수, n = 전체 관측치의 수
-
-
$MSB = \frac{SSB}{k-1}$
-
$MSW = \frac{SSW}{n-k}$
-
일원분산분석의 절차
-
가설 설정
-
유의수준
-
검정통계량 선택 : $F = \frac{MSB}{MSW}$ $\sim F(k-1, n-k)$
-
임계값 및 기각영역 결정 - 기각역: $F > F_\alpha$ (우측검정)
-
분산분석표(ANOVA Table)작성 및 결론

Reference
-
- Lind, Marchal, Wathen, (2018), McGrawHill, 강종열 등 역, 지필미디어