이 글은 경영학부 경영통계 수업에서 배운 자료들을 정리한 내용입니다.
- Key Point : 균등분포, 정규분포, 표준정규분포
Contents
-
균등분포를 활용하여 확률을 계산한다.
-
정규분포의 특징을 파악한다.
-
표준정규분포를 활용하여 확률을 계산한다.
-
표준정규분포를 활용하여 이항 분포의 확률값을 근사적으로 계산한다.
이산확률변수 vs 연속확률변수
-
이산확률변수(Discrete random variable)-
어떤 정해진 값만 가질 수 있고 값들 사이에 간격이 있는 변수
-
주로 수를 세어서(counting) 값을 할당
-
-
연속확률변수(Continuous random variable)-
주어진 구간 내에서 어떤 실수 값이라도 가질 수 있는 변수
-
주로 측정(measurement)에 의해 값을 할당
-
연속확률분포(Continuous probability distribution)
-
연속확률분포
-
연속확률변수의 확률분포: 주어진 구간 내 무한 개의 측정값이 가능
-
균등분포, 정규분포
-
-
연속확률분포의 특징
-
특정한 하나의 값이 나타날 확률 = 0
-
특정 구간의 확률 만이 의미가 있음
-
부등호, 등호의 유무 차이가 없음 ⇒ P(a≤X≤b) = P(a<X<b)
-
-
특정 구간의 값이 나타날 확률은 0 ~ 1 사이
-
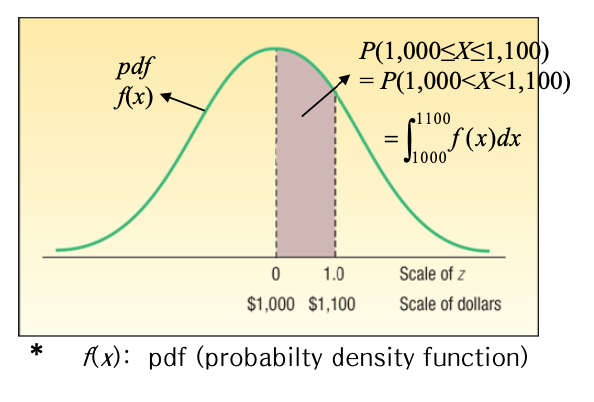
모든 가능한 값들을 포함하는 총 확률 = 1 < = > 전체 넓이 : 1
-
f(x) : pdf(probability density function) : 확률밀도함수
-
균등분포(Uniform Probability distribution)
-
균등분포
-
연속확률변수를 묘사하는 가장 간단한 확률분포
-
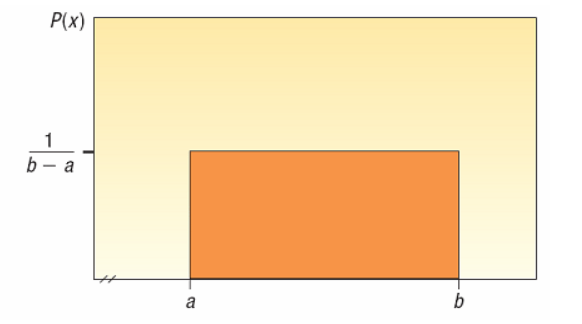
균등분포는 최소값 (a)과 최대값 (b)으로 규정된 범위 내의 모든 지점에서 확률밀도함수 f(x)의 값이 일정
-
최대값과 최소값 사이에 모든 확률이 존재, 그 범위 외에는 존재 확률 = 0
-
평균 = 중위수 (동일)
-
-
예1) 뉴욕에 있는 퀵 필 사에서 하루에 판매되는 가솔린의 양은 최소 2,000 ~ 최대 5,000 갤런사이의 균등분포를 따른다고 한다.
-
확률변수는 하루에 판매되는 가솔린의 양이며,
-
분포함수는 2,000 ~ 5,000 갤런 사이의 연속함수이다.
-
-
예2) 공공도서관의 자원봉사자는 연방세금신고서를 작성하는 것을 도와주고 있다. 세금신고서 서류를 한 부 작성하는데 최소 10분, 최대 30분의 시간이 소요되며 균등분포를 따른다
-
확률변수는 한 부의 서류를 작성하는데 걸리는 시간
-
분포함수는 10 ~ 30 사이의 어떤 실수 값을 가진다.
-
균등분포_pdf, 평균, 분산, 확률
-
pdf
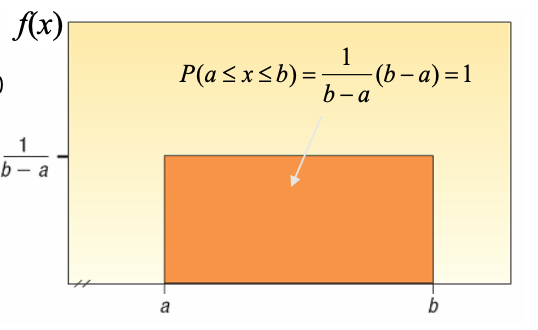
$f(x) = \ {1 \over b-a}$
-
a ≤ x ≤ b 구간 내에서만, 구간 외 f(x) = 0
구간 내 ⇒ 최소값: a, 최대값: b
-
균등분포의 평균, 분산, 표준편차
$\mu = {a+b \over 2} \ \sigma^2 = {(b-a)^2 \over 12} \ \sigma = \sqrt{\sigma^2}$
- $x_1 과\ x_2\ 사이의\ 확률\ (단, a ≤ x_1, x_2 ≤ b)$
$P(x_1 ≤ x ≤ x_2) = {1 \over b-a}(x_2 - x_1)$
- 균등분포의 확률분포함수
$P(x) = {1 \over b-a} \a ≤ x ≤ b 이면, 아니면 0$
정규분포(Normal probability distribution)
- 정규분포
$f(x) = {1 \over \sigma\sqrt{2 \pi} }e^-{(x-\mu)^2 \over 2\sigma^2}$
-
정규분포의 특징
-
종모양, 중앙에 하나의 정점을 가짐
-
평균을 중심으로 대칭으로 분포됨
-
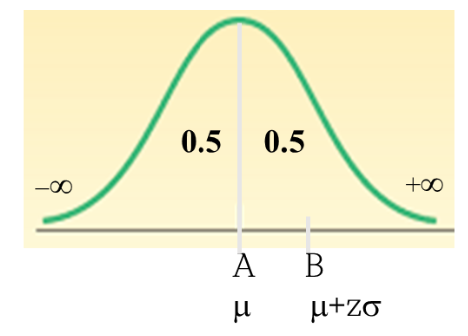
좌, 우 각각 50%(0.5)씩 확률을 가진다.
-
평균 = 중위수 = 최빈값
-
-
정규분포의
위치는 평균인 $\mu$ 에 의해 정의됨 -
정규분포의
산포는 표준편차 $\sigma$ 에 의해 정의됨 -
수평축 양 끝으로 갈수록 곡선은 수평축에 점근하나(asymptotic), 절대 만나지 않으며 무한대까지 이어진다.
-
-
정규분포의 모양 및 위치
-
표준편차의 증가 ⇒ 분포의 모양이 평평해짐
-
평균에 의해 분포의 위치가 결정됨
-
표준정규분포(Standard Normal Probability Distribution)
-
표준정규분포
-
z 분포라고 불림
-
평균 = 0, 표준편차 = 1 인 정규분포
-
-
표준화(Standardization)
-
$f(x) = {1 \over \sigma\sqrt{2 \pi} }e^-{(x-u)^2 \over 2\sigma^2} => f(z) = {1 \over \sqrt{2 \pi} }e^{-z^2 \over 2}$
-
$z = {X -\mu \over \sigma}$
-
X: 특정관측치 (ex 주당 수입, 자동차 배터리의 수명)
-
-
z값 변환 통한 표준화(standardization) : 정규분포의 표준정규분포로의 변경
-
$X \thicksim N(\mu, \sigma^2) → Z \thicksim N(0,1)$
-
참고 ) 표준정규분포표 → “시험”에서는 주어진다. (p.18 참고)
-
-
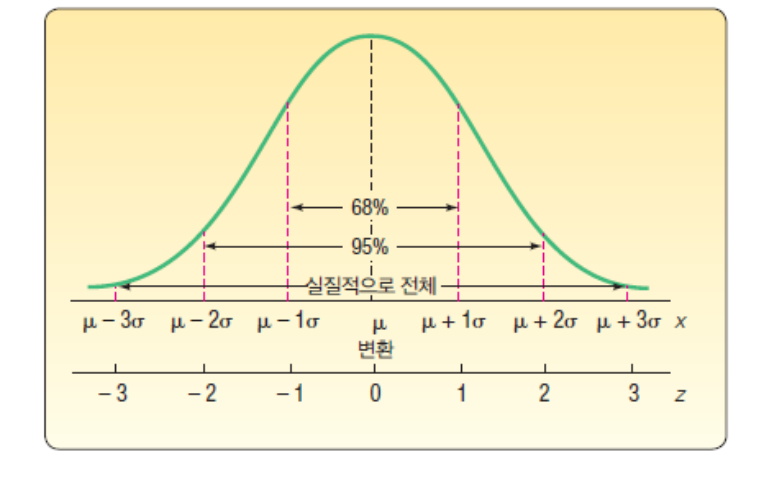
경험적 법칙
-
정규분포데서 관측값의 약 68%는 평균을 중심으로 표준편차 1배의 값 사이에 있다.
-
정규분포데서 관측값의 약 95%는 평균을 중심으로 표준편차 2배의 값 사이에 있다.
-
정규분포데서 관측값의 약 99%는 평균을 중심으로 표준편차 3배의 값 사이에 있다.
이항분포의 정규 근사
-
다음 조건을 만족할 경우 정규분포를 활용하여 이항분포의 확률값을 근사적으로 구할 수 있음
- $n\pi$ 와 $n(1-\pi)$의 값이 모두 최소 5이상
-
이항분포가 되기 위한 조건들
-
시행의 결과는 2가지 중 한가지로만 나타남
-
성공확률 $\pi$ 는 시행마다 항상 불변
-
모든 시행은 모두 상호 독립적임
-
확률변수는 전체 시행횟수에서 성공횟수를 나타냄
-
-
이항 분포 공식
- $P(X) = \ {_n}\mathrm{C}{_x} \pi^x(1-\pi)^{n-x}$
-
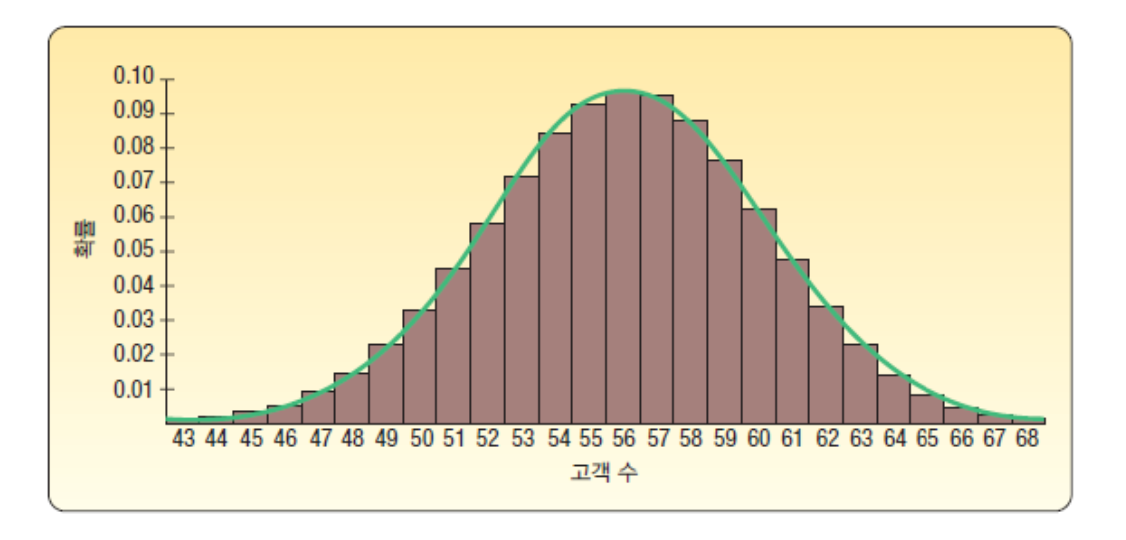
연속성 보정계수
-
연속 확률분포를 이용해서 이산분포를 계산할 때 문제의 성질에 따라 0.5를 더하거나 빼야만 한다.
-
이렇게 보정된 0.5의 값을 연속성 보정계수라고 한다.
-
-
보정계수 적용방법
-
[1] x 이상의 확률을 계산할 때는 (x - 0.5)보다 큰 면적을 계산
- 예) 56이상 → (56-0.5) = 55.5 = x 값
-
[2] x를 초과 → (x + 0.5)
-
[3] x 이하 → (x + 0.5)
-
[4] x 미만 → (x - 0.5)
-
Reference
-
- Lind, Marchal, Wathen, (2018), McGrawHill, 강종열 등 역, 지필미디어