이 글은 경영학부 경영통계 수업에서 배운 자료들을 정리한 내용입니다.
Contents
-
모평균에 대한 점추정을 구하고 해석한다.
-
모평균에 대한 신뢰구간을 구하고 해석한다.
-
모비율에 대한 신뢰구간을 구하고 해석한다.
-
모평균과 모비율을 추정하기 위해 필요한 표본크기를 계산한다.
모평균에 대한 점추정
- 점추정(Point estimate): 표본 통계량으로부터 모수의 단일 값을 추정
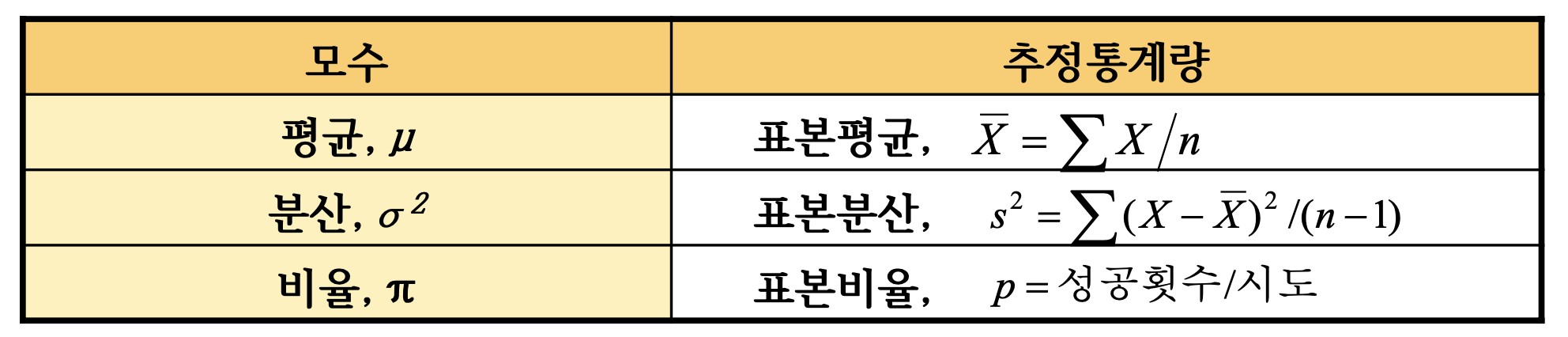
모평균에 대한 신뢰구간
-
구간추정(Interval esitmate): 모수의 실제값이 들어 있을 구간을 추정
-
모평균 → $\sigma$ 알려짐 / $\sigma$ 알려지지 않음
-
모비율
-
-
신뢰구간(Confidence interval)
-
어떤 구간(하한, ,상한)내에 모수의 실제값이 있을 것으로 추정되는 구간 값
-
신뢰수준, ($1-\alpha$)
-
$\alpha$ : 유의 수준(significance level)
-
$1-\alpha$ : 신뢰수준(confidence level)
-
예) 유의수준 $\alpha$ = 5% ⇒ 95% 신뢰구간
-
신뢰구간 = 점추정량 $\pm$ 오차범위
-
-
-
모평균에 대한 신뢰구간의 폭(오차범위)을 결정하는 요인
[1] 표본수 : 표본 크기 n이 증가할수록 신뢰구간 폭이 좁아진다.
[2] 모집단의 표준편차, 모를 경우 표본표준편차 : 표준편차가 클수록 신뢰구간 폭이 넓어진다.
[3] 원하는 신뢰수준: 신뢰수준이 클수록 신뢰구간 폭이 넓어진다.
신뢰구간 도출 과정
-
[1] 신뢰수준을 설정한다. (주로 문제에 주어짐, ex) 95%)
-
[2] $\alpha$ 와 $\alpha / 2$ 계산 ⇒ $1-\alpha$ = 0.95, $\alpha$ = 0.05
-
[3] 대응하는 Z값을 찾는다 : $Z값$ → $Z_{0.025}$ = 1.96
-
[4] 오차범위(margin of error)를 구하기 위해 Z값에 표준오차를 곱한다.
$Z_{\alpha / 2} = \frac{\sigma}{\sqrt{n}}$
- [5] 표본평균에 오차범위를 더하고 빼서 신뢰구간을 결정한다.
$( \bar{X} - 1.96\frac{\sigma}{\sqrt{n}}, \bar{X} + 1.96\frac{\sigma}{\sqrt{n}} )$
T분포
t분포의 특성
-
$\sigma$ 대신 $S$로 표준화를 할 경우, 표준정규분포를 따르지 않음.
-
종모양 대칭의 연속확률분포
-
자유도(df, degree of freedom)에 따라 모양이 결정되어 여러개의 분포가 존재함
- df = n - 1
-
t분포는 z분포에 비해 평평한 분포를 가짐.
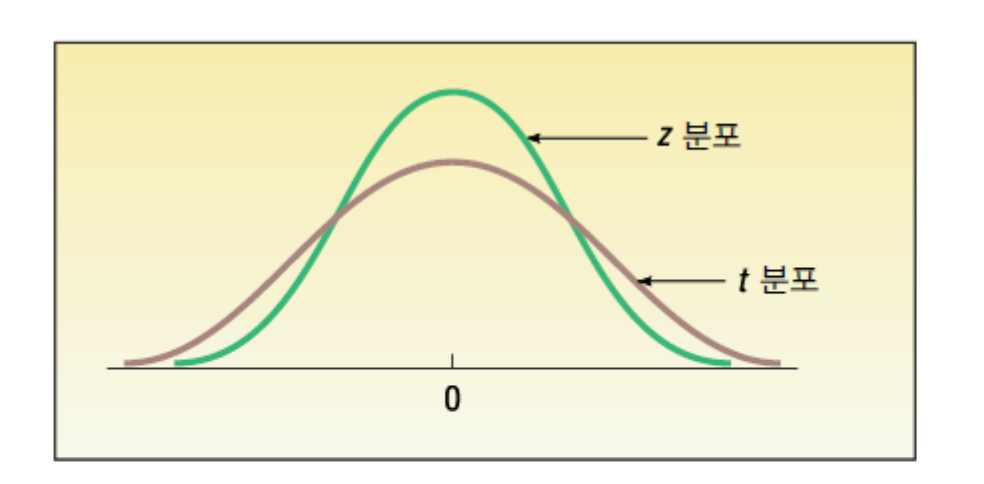
- 표본크기 n의 증가함에 따라 폭이 좁아져 z분포에 가까워짐
자유도(df)
-
어떤 데이터 집합 내에서 자유로운 값들의 수
-
예) n=4, 표본 평균 = 10일때
-
자유도 = 3 = (n-1)
t값 구하기 (중요)
-
모집단의 분포가 정규분포라고 가정
-
자유도(df)값을 구한다. ⇒ df = n - 1(표본크기 n = 10 → 자유도 = 9)
-
$\bar{X} \pm t_{n-1} \frac{s}{\sqrt{n}}$
-
t 분포표 에서 해당 신뢰구간에 대한 t값을 구한다.
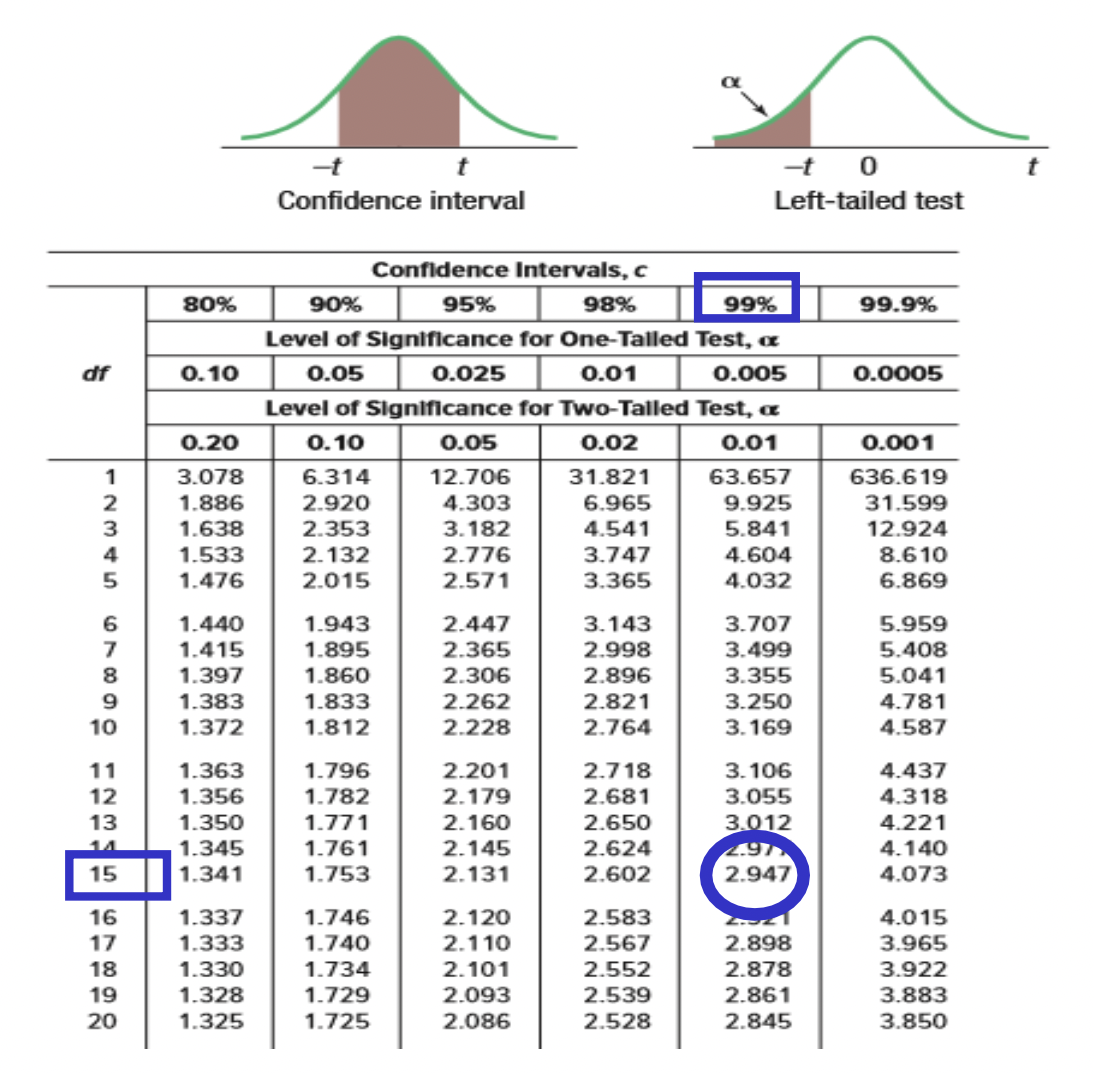
모비율에 대한 신뢰구간 (중요)
-
표본비율: $p = \frac{x}{n}$ (⇒ 모비율에 대한 점추정치)
-
표본비율의 표본분포(Sampling distribution of the sample proportion)
-
$\mu = n\pi, \sigma^{2} = n\pi(1-\pi)$
-
$\pi$ : 성공확률
-
표본비율의 표본분포의 평균과 분산
-
평균 E(p) = $\pi$
-
분산 V(p) = $\frac{\pi(1-\pi)}{n}$
-
-
-
모비율 추정 시 중심극한정리 적용을 위한 조건
- np ≥ 5이고 n(1-p) ≥ 5 일때 → 중심극한정리 적용, 표준정규분포(z) 활용
-
모비율에 대한 구간 추정 (중요)
- 모비율 $\pi$ 의 신뢰구간 = $p \pm z\sqrt{\frac{p(1-p)}{n}}$
표본크기 결정 (중요)
-
구간추정에서 표본크기를 정할 때 고려요인
-
오차한계(E): 신뢰구간의 폭을 좁히기 위해서는 작은 오차한계가 필요하며 이를 위한 표본크기는 커지게 됨 ⇒ $E = X - \mu$
-
원하는 신뢰수준: 신뢰수준이 커질 수록, 필요한 표본크기는 커짐
-
모집단의 변동성: 모표준편차가 커지면, 더 많은 표본자료가 필요함
-
-
구간추정에서 사용된 오차한계(E)를 통해 표본크기를 정할 수 있다.
-
모평균에 대한 구간추정 : $E = z\frac{\sigma}{\sqrt{n}}$ ⇒ $n = ({\frac{z\sigma}{E}})^{2}$
-
모비율에 대한 구간추정: $E = z\sqrt{\frac{p(1-p)}{n}}$ ⇒ $n = p(1-p)(\frac{z}{E})^{2}$
-
모분산과 표본분산을 모른다면? ⇒ 자료의 범위 사용 : R = 4$\sigma$ ↔ $\sigma = \frac{R}{4}$)
-
Reference
-
- Lind, Marchal, Wathen, (2018), McGrawHill, 강종열 등 역, 지필미디어