- Contents
- 가설과 가설검정
- 귀무가설, 대립가설
- 검정통계량, 기각역
- 가설 검정의 종류
- 가설검증 단계
- 한쪽 꼬리검정과 양쪽 꼬리 검정
- 모평균에 대한 가설검정
- p-값을 이용한 가설검정
- 모비율에 대한 가설검정
- Reference
이 글은 경영학부 경영통계 수업에서 배운 자료들을 정리한 내용입니다.
Contents
-
가설검정 과정을 설명한다.
-
여섯 단계의 가설검정 과정을 적용한다.
-
한쪽꼬리검정과 양쪽꼬리검정을 구별한다.
-
모평균에 대한 가설검정을 수행한다.
-
P-값을 계산하고 해석한다.
-
가설검정을 위해 t 통계량을 사용한다.
가설과 가설검정
-
가설(Hypothesis)
- 모집단의 모수에 대한 진술, 주장, 표본추출을 통한 통계분석으로 검정해야 할 대상
-
가설검정(Hypothesis testing)
- 모수에 대한 어떤 가설을 수립하고 수집된 표본정보를 이용해 가설의 옳고 그름을 판정하는 과정
귀무가설, 대립가설
-
두 가설은 항상 함께 표현되며, 서로 여집합의 관계 (서로 상호배타적이며 포괄적)
-
귀무가설($H_{0}$, Null hypothesis)
-
수치증거를 검정하기 위한 목표로 만들어진 모집단 모수 값에 대한 진술
-
현재 진실로 받아들여지고 있는 사실 또는 일반적으로 알려져 있는 내용
-
등호가 항상 포함됨(”=”, “≥”, “≤”)
-
-
대립가설($H_{1}$, Alternative hypothesis) == 연구가설(research hypothesis)
-
표본의 데이터 정보가 귀무가설이 거짓이라는 충분한 증거를 제시할 때 채택되는 진술
-
귀무가설을 부정함으로써 새롭게 입증하려는 내용
-
등호를 포함하지 않음. (”<”, “>”, “ $\ne$”)
-
검정통계량, 기각역
-
검정통계량(test statistic) → 귀무가설 “결백”
-
가설검정을 위해 사용되는 통계량. Ex) $z, t, F, \lambda^{2}$
-
가설검정은 항상 귀무가설이 사실이라는 전제하에 진행됨
-
-
기각역(rejection region)
-
귀무가설을 기각할 수 있는 검정통계량 값의 범위
-
추출된 표본으로부터 검정통계량 값이 이 기각역에 들어가면 귀무가설을 기각하고, 대립가설을 채택하게 됨.
-
가설이 $\ne$ 형태 → 양쪽꼬리(양측)검정(two-sided test)
-
가설이 “<”, “>” 형태일 때는 한쪽꼬리(단측)검정(one-sided test)
-
기각역이 넓으면 귀무가설을 기각할 가능성이 높아짐(기각역의 범위가 넓어지기 때문이다)
-
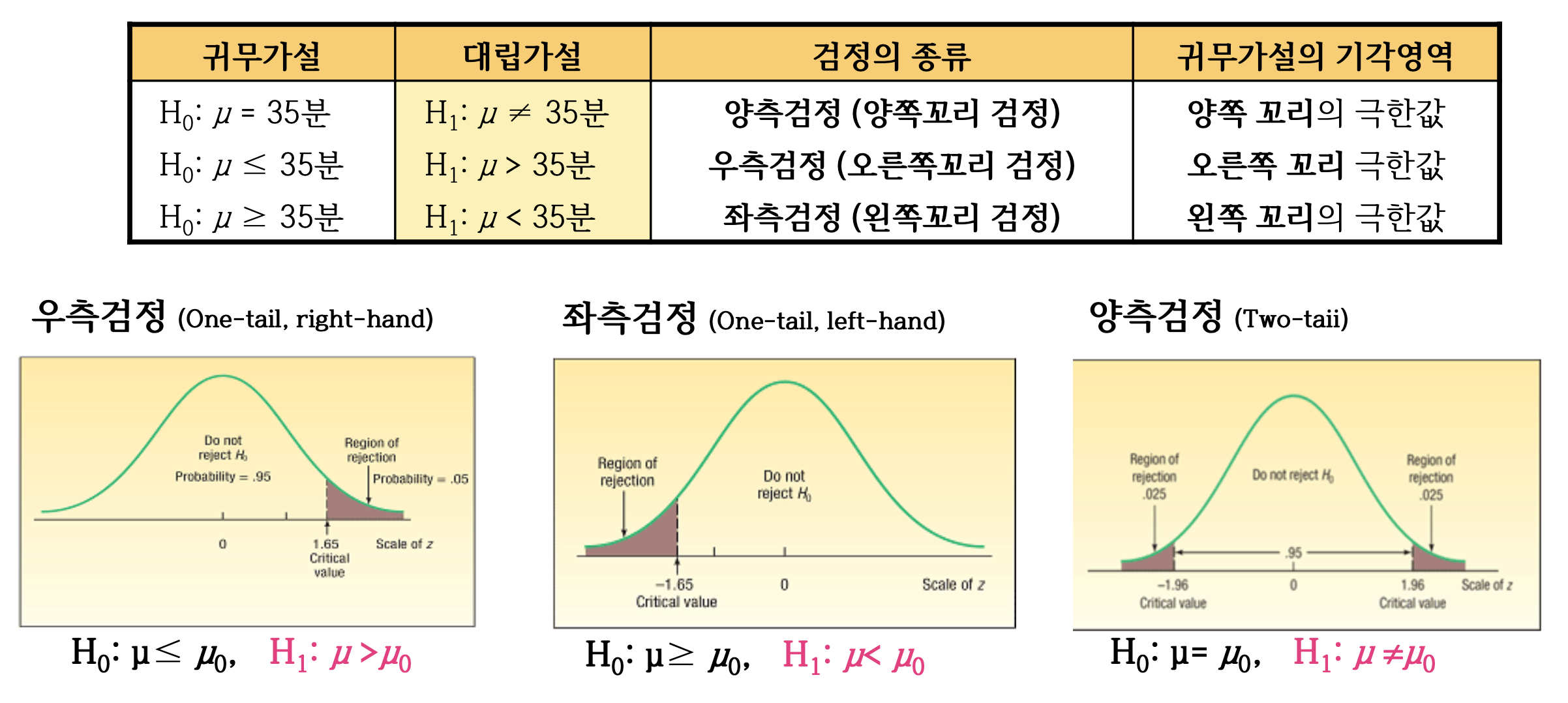
가설 검정의 종류
-
가설 검정의 종류
-
양쪽꼬리(양측)검정
-
한쪽꼬리(단측)검정 : 대립가설의 기호의 방향을 따름.
-
-
가설검정의 목적 및 결론
-
귀무가설에 검증이 필요하기 때문
-
일단 귀무가설이 맞다는 가정 하에 가설 검정을 수행
-
귀무가설을 기각할 수 있으면 → 강한 결론(strong conclusion): 귀무가설을 기각하고 대립가설을 채택
-
귀무가설을 기각할 수 없으면 → “증거가 불충분하므로 무죄를 선언한다”
-
가설검증 단계
-
1단계 : 가설의 설정 → 귀무가설 & 대립가설
-
2단계: 유의수준 결정 → $\alpha$ = 0.05 or 0.01
-
3단계: 검정통계량 선택 → z or t
- $z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}}$ or $z = \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}}$ or $t= \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}}$
-
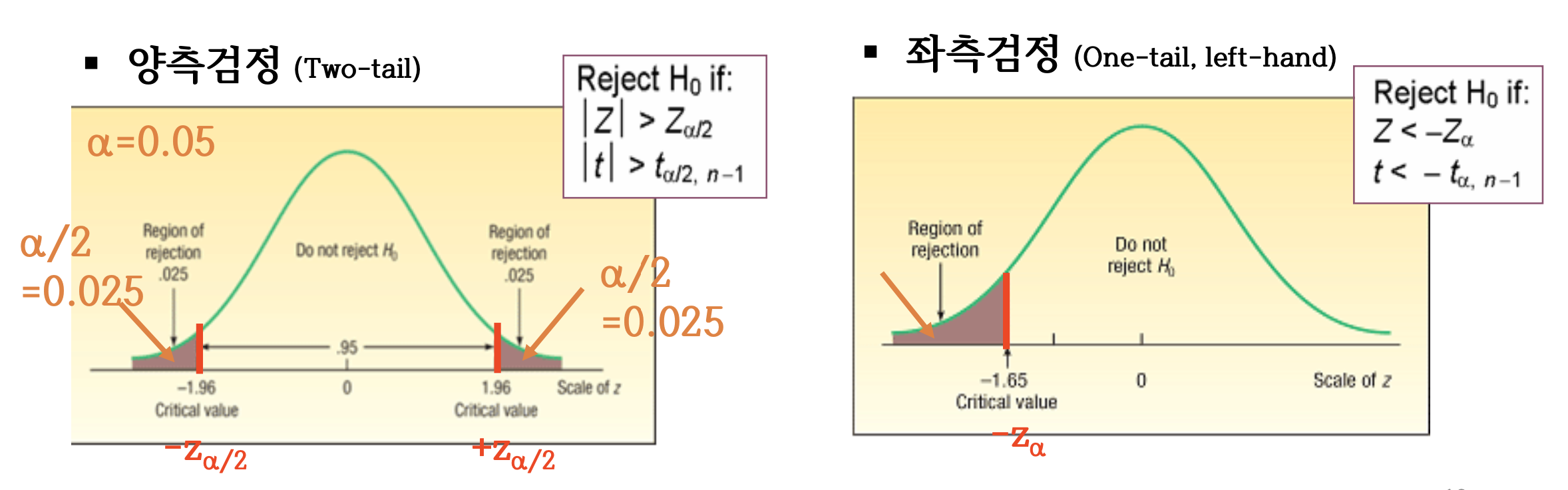
4단계: 임계값 및 기각영역 결정
- 임계값: $\alpha$에 대항하는 양측일 때 → $z_{\alpha/2}$ or $t_{\alpha/2}$ / 한쪽일 때 → $z_{\alpha}$ or $t_{\alpha}$
-
기각영역: 임계값이 결정
-
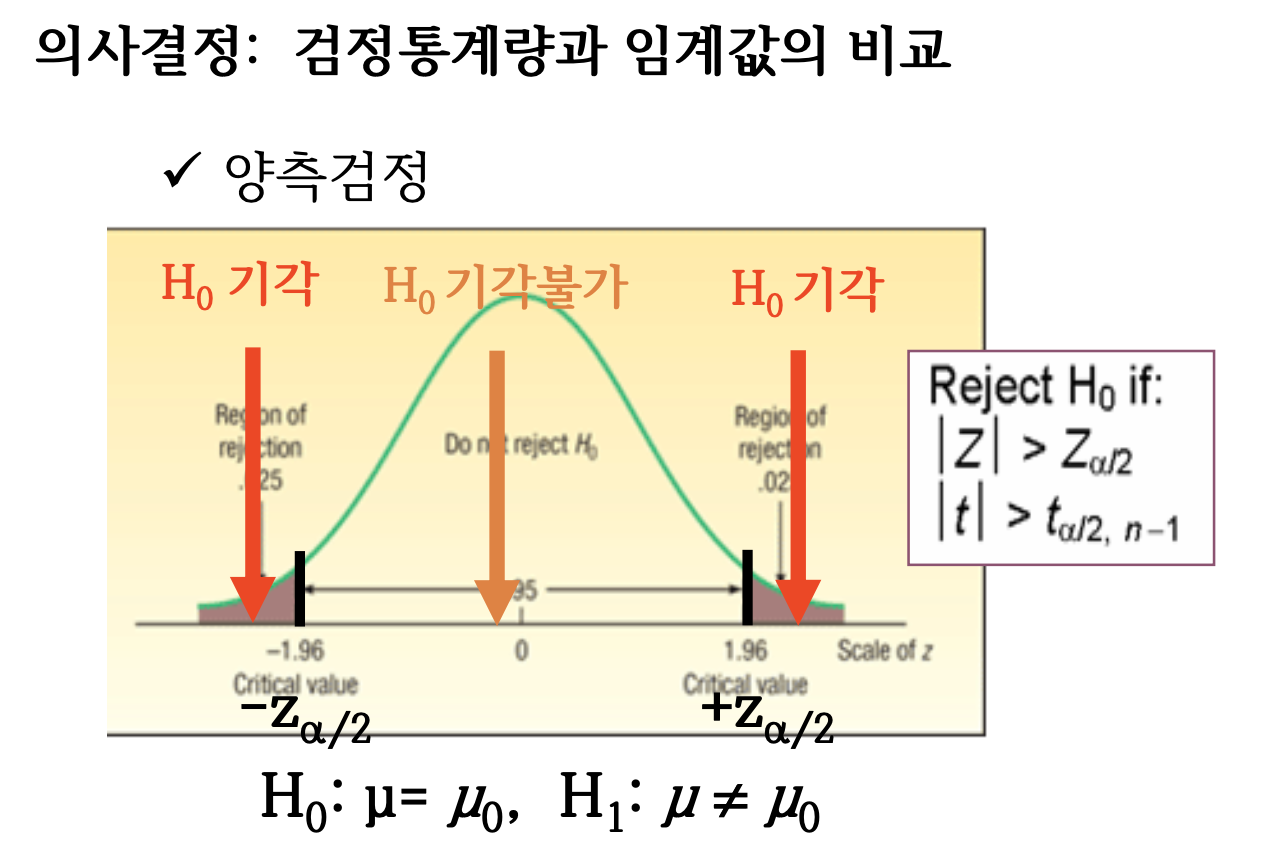
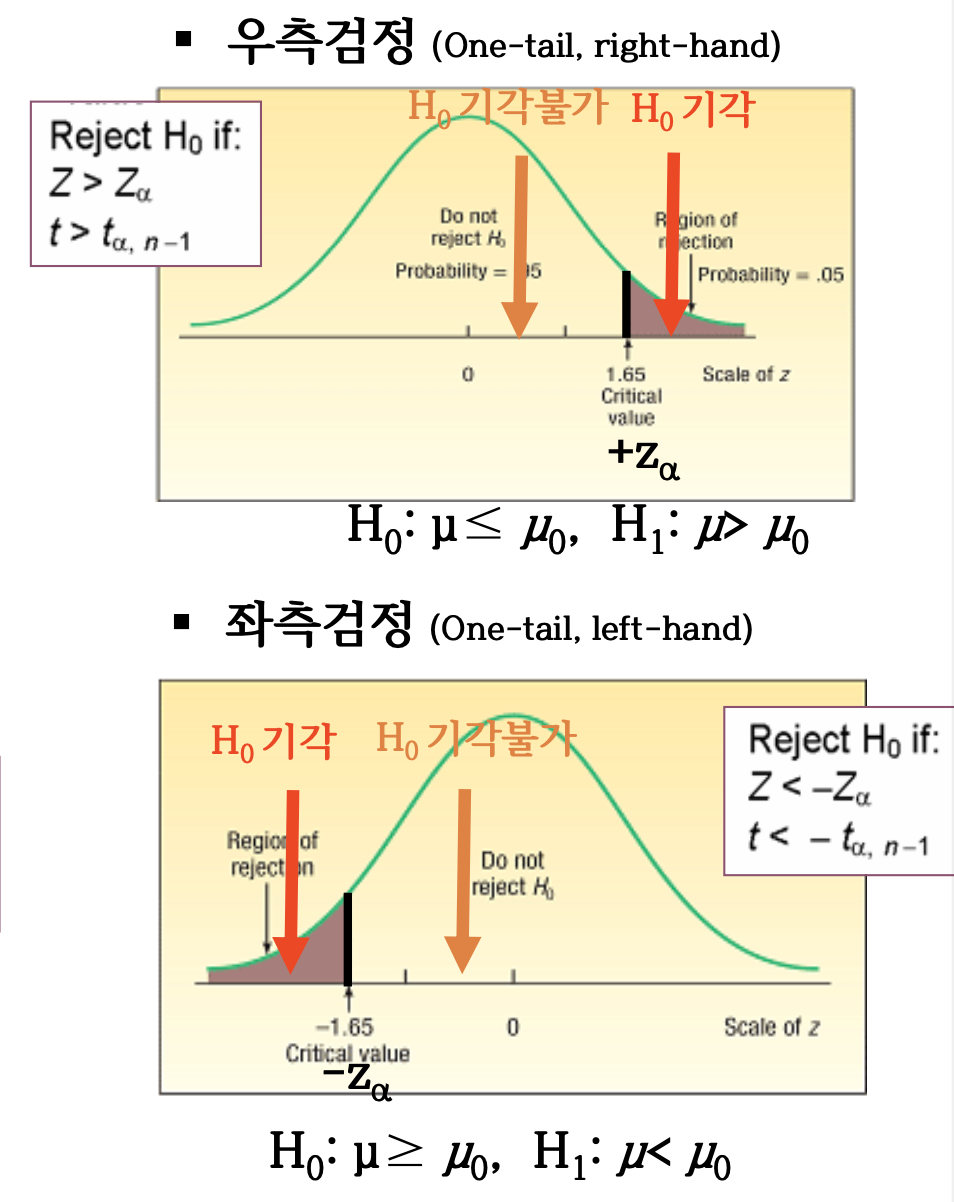
5단계: 귀무가설의 기각여부 결정
-
검정통계량 계산
-
임계값 또는 기각영역과 비교
-
한쪽 꼬리검정과 양쪽 꼬리 검정
-
한쪽 꼬리 검정 ⇒ 왼쪽 or 오른쪽
-
양쪽 꼬리 검정
-
예) 정규분포의 면적은 1이다.
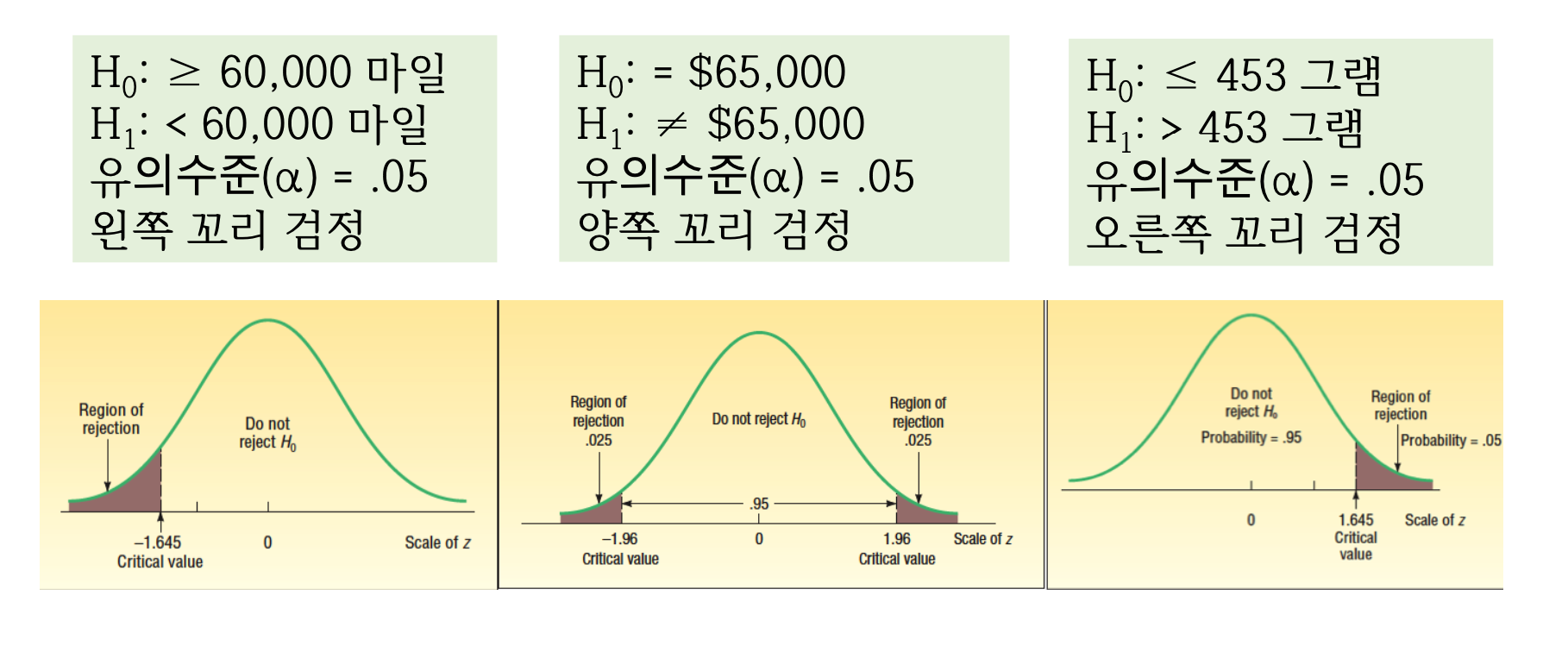
모평균에 대한 가설검정
-
모표준편차($\sigma$)을 아는 경우 → z 분포 - 양쪽 꼬리 검정 또는 한쪽 꼬리 검정
-
모표준편차($\sigma$)을 모르는 경우 and n < 30인 경우 → t 분포- 양쪽 꼬리 검정 또는 한쪽 꼬리 검정
- 조건: n < 30 이고, 모표준편차를 모르는 경우 t 분포를 사용한다.
-
t 분포의 주요 특징
-
종모양의 좌우대칭형 연속분포이다.
-
자유도가 변할 때마다 새로운 분포가 형성된다.
-
자유도가 증가함에 따라 t 분포의 모양은 표준 정규분포의 모양에 가까워진다.
-
표준 정규분포보다 더 평평한 모양을 가짐 → z 분포보다 더 큰 값을 가진다.
-
p-값을 이용한 가설검정
-
p-값: 귀무가설이 참이라고 가정할 때 실제 관측지보다 극단적인 결과가 실제로 관측될 확률 -
p-값은 $H_{0}$ 이 거짓이라는 가능성을 표현하는 방식임
-
p-값과 유의수준($\alpha$)을 비교 → 유의수준보다 작으면 $H_{0}$ 기각함.
-
정리
-
[1] 검정통계량(z값, t값)에 해댱하는 꼬리 쪽의 확률 → p-값
-
[2] 그런 p-값과 유의수준을 비교하여 작으면 귀무가설을 기각하고, 아니면 기각하지 않는다.
-
모비율에 대한 가설검정
Step 1, 3 ⇒ Step1(가설 설정)과 Step3(검정통계량)에 수정을 제외하고 나머지 순서는 같다.
-
Step 1: 모비율 $\pi$ 를 이용한 가설 검정 ⇒ 대립가설로 방향 결정하는 것은 같다.
-
Step 3: 검정통계량 선택 ⇒ $\mu = \pi, \sigma^{2} = \pi(1-\pi)/n$ 이용
-
귀무가설이 참이라는 가정하에 검증시작( 항상 모분산이 주어짐)
-
z 분포를 사용할 수 있음
-
Reference
-
- Lind, Marchal, Wathen, (2018), McGrawHill, 강종열 등 역, 지필미디어