- Contents
- 전수조사와 표본조사
- 표본추출법(Sampling Method)
- 표본오차
- 표본평균의 표본분포
- 중심극한정리(Central Limit Theorem, CLT)
- 표본평균의 확률분포의 활용
- 표본비율의 분포
- Reference
이 글은 경영학부 경영통계 수업에서 배운 자료들을 정리한 내용입니다.
Contents
-
표본을 추출하는 이유, 4가지 표본추출법
-
표본오차 정의
-
표본평균의 표본분포 정의
-
중심극한정리의 정의 → 표준오차 정의
-
중심극한정리를 활용 → 확률 계산
전수조사와 표본조사
-
전수조사: 대상 모집단의 모든 구성원소를 전부 조사 -
표본조사: 모집단으로부터 추출된 일부만을 조사, 표본추출의 종류-
[1] 확률추출(Probability sampling)**
-
표본 추출 시 주관적 판단이 개입되지 않음.
-
종류 4가지 - 단순무작위 추출, 체계적 추출, 층화 추출, 군집추출
-
-
[2] 비확률 추출(Non-probability sampling)
- 주관적 판단에 의해 표본 추출(직관 및 재량)
-
표본추출법(Sampling Method)
단순 무작위 추출법(Simple Random Sampling)
-
표본으로 선택될 가능성이 모집단에 속한 모든 요소에 의해 동일한 조건에서 추출된 표본
-
어떤 한 개체의 선택이 다른 개체의 선택에 영향을 미치지 않도록 추출
-
시간이 많이 소요될 수 있고 표본이 편중될 가능성을 완전히 배제할 수 없음
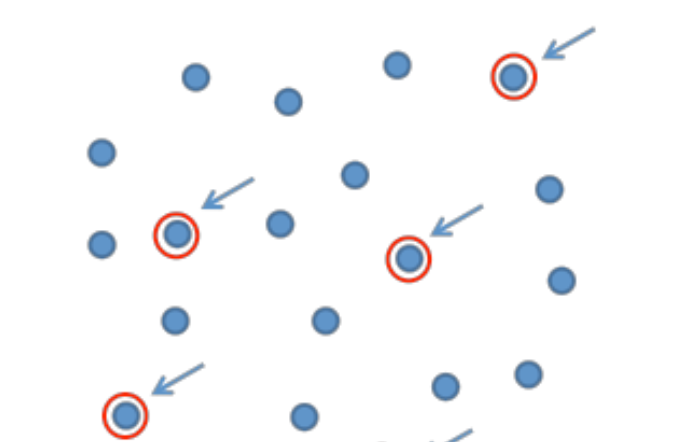
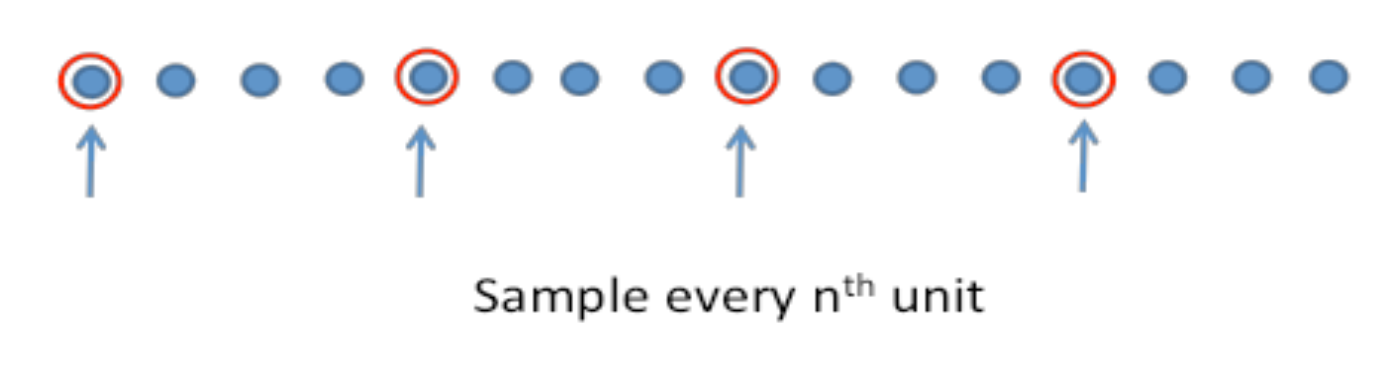
체계적 추출법(Systematic Random Sampling)
-
임의로 시작지점을 선택한 후 모집단에서 그 다음 매 k번째 요소를 선택하는 방식으로 추출된 표본(k = N/n 으로 정함)
-
주기성(periodicity)의 문제가 있을 수 있음
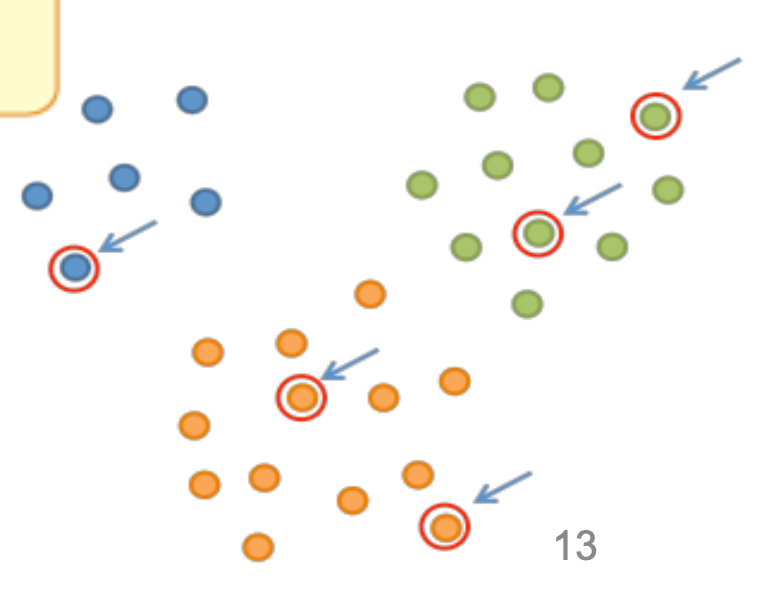
층화 추출법(Stratified random sampling)
-
모집단을 층(strata)이라 부르는 몇 개의 집단으로 나누고 각 층에 대해 무작위 추출을 시행하여 얻은 표본
-
각 층내에서는 기본 단위 특성이 균일하고, 층 별로는 차이가 클 때 사용
-
전체 대비 각 계층에 속한 모집단 수의 비율을 구함
-
추출할 각 집단의 표본수를 위에서 구한 비율로 결정
-
각 집단 별로 정해진 수 만큼 단순임의표본을 추출
-
예시) 교육수준에 따른 층화 표본의 수 결정(표본 수 n = 1000)
학력 1. 모집단 2. 비율 3. 층화표본수 3. 층화표본수(반올림) 고졸 미만 10466000 9.46% 94.5 95 고졸 이상 34011000 30.74% 307.3 307 대학 중퇴 31298000 28.29% 282.8 283 대졸 34874000 31.52% 315.1 315 전체 110649000 100% 1000 1000
군집 추출법(Cluster sampling)
-
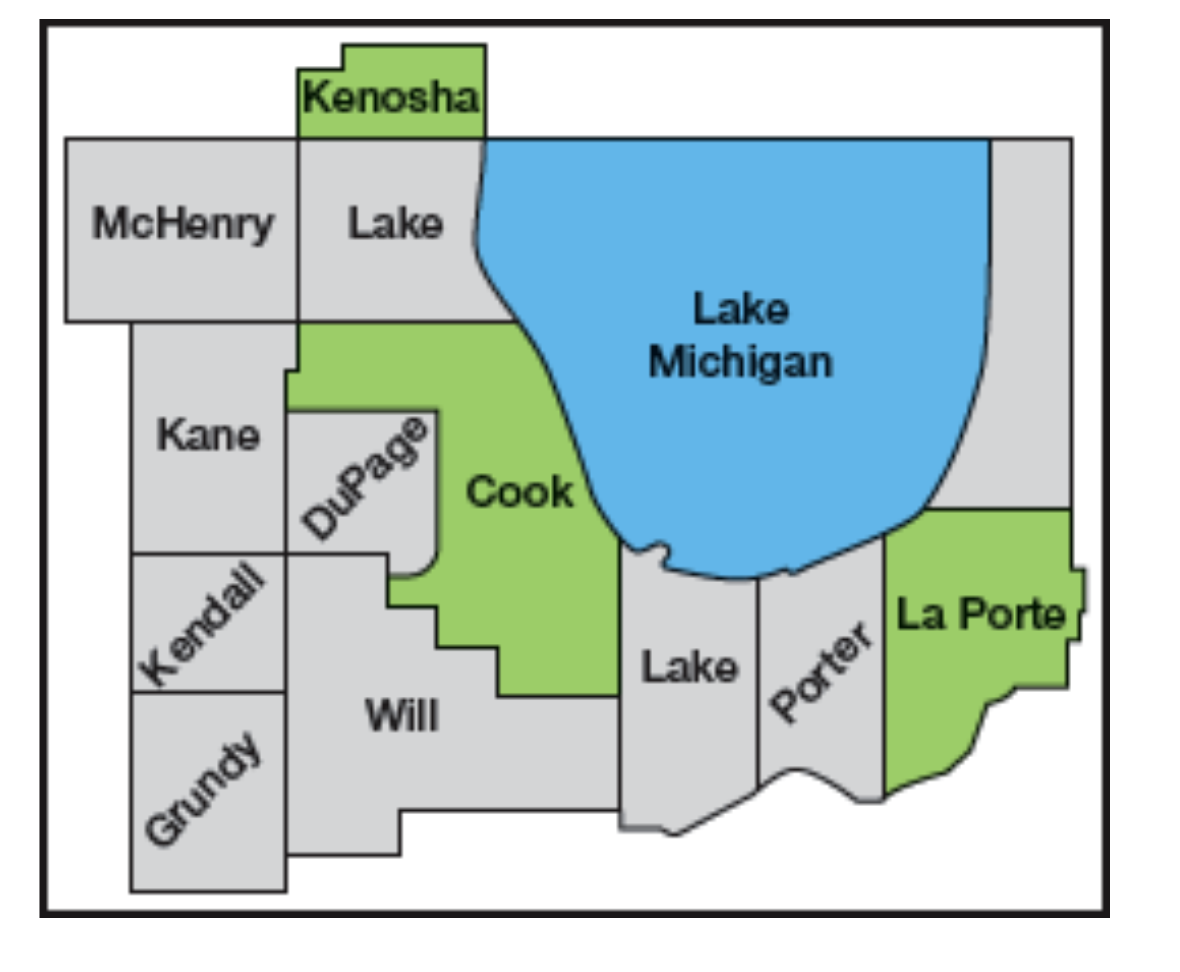
모집단이 지리적 또는 다른 기준에 의해 여러 개의 지역으로 구분되는 경우에, 그 중 몇개의 지역을 무작위로 선택하고 선택된 지역으로부터 무작위로 추출된 표본
-
예시) 미국 광역시카고의 12개 카운티에 거주하는 주민들의 의견조사
-
모집단이 넓은 지역에 퍼져있는 경우 효율적 표본 추출 방법이 될 수 있음
-
군내에서는 기본 단위 특성차이가 크고 군간 차이가 작을때 사용
표본오차
-
모집단의 일부분인 표본에 의해서 전체의 특성을 파악하려는 데서 오는 오차
-
전수조사에서는 발생치 않음
-
비용, 시간등의 현실적인 제약요건 존재
-
정의: 표본통계량과 이에 대응하는 모집단 모수 간의 차이 ⇒ 모평균 - 표본평균
표본평균의 표본분포
-
간단히 말하면, 표본의 평균값들을 분포로 나타낸 것
-
같은 크기로 가능한 모든 표본을 추출하여 평균값을 구하면, 표본평균분포를 기대할 수 있음.
-
정의: 동일한 크기의 모든 가능한 표본들로 얻어진 표본평균들의 확률 분포
-
표본평균의 평균: 표본평균들의 합 / 표본의 숫자
- 표본의 숫자 ⇒ 조건부확률(${n}\mathrm {C}{k}$)
-
표본평균의 표본분포의 평균과 표준오차
-
평균= $\mu$ -
표준오차= $\frac{\sigma }{\sqrt{n}}$
-
-
n이 증가하면 표준오차가 작아져 표본분포가 좁아지게 된다.
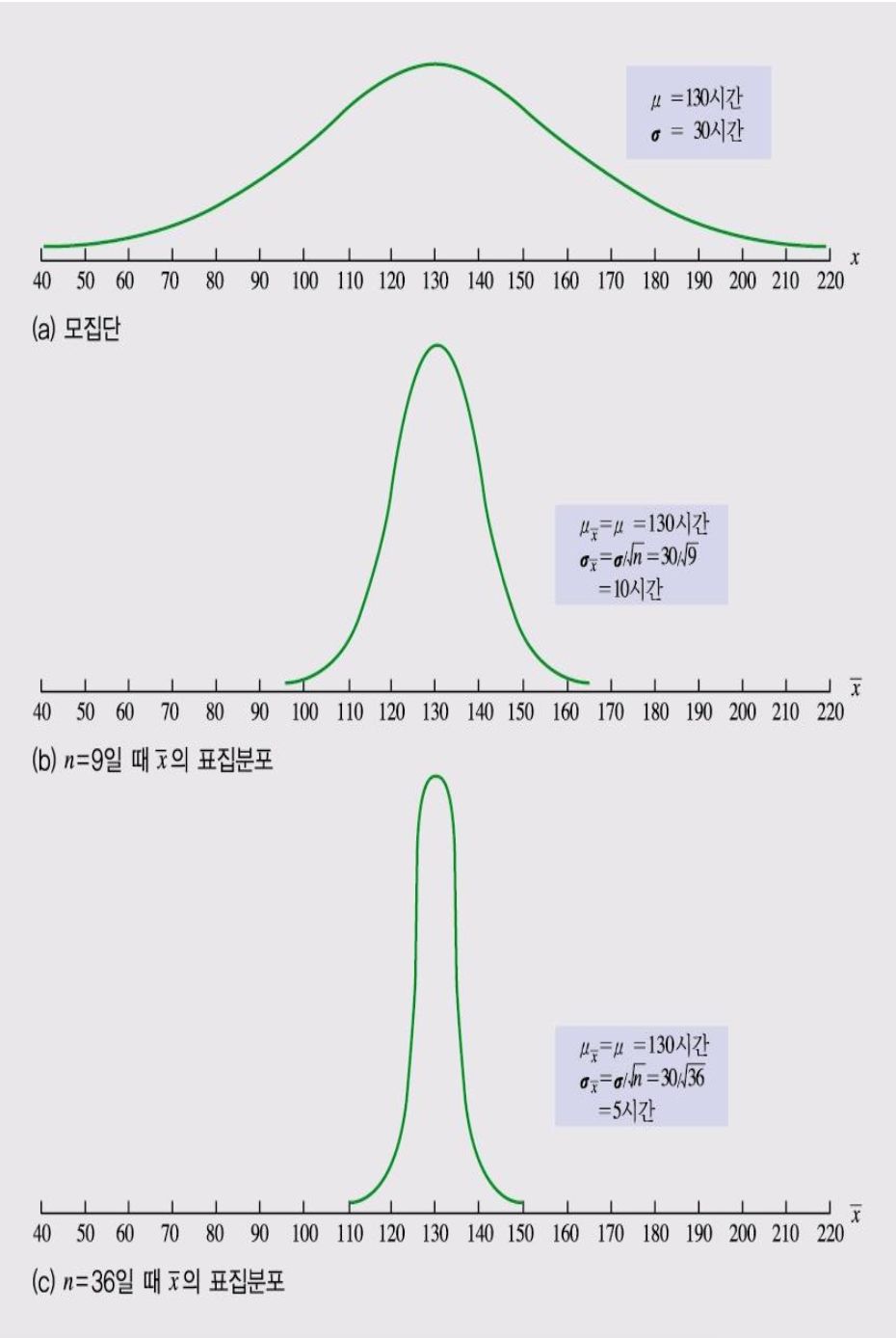
중심극한정리(Central Limit Theorem, CLT)
-
어떤 모집단으로부터 동일한 크기의 모든 가능한 표본들을 추출하고, 이로부터 표본평균분포를 구하면 정규분포에 근사하게 된다. 이러한 근사화는 표본의 크기가 커질수록 더욱 강화된다.
-
$\bar{X} \sim N ( \mu, ( \frac{\sigma}{\sqrt{n}})^2 )$
-
z = $\frac{\bar{X} - \mu}{\sigma / \sqrt{n}}$
표본평균의 확률분포의 활용
-
n > 30 일때 (중심극한 정리에 근거)
-
모 표준편차 $\sigma$ 을 알 때의 표준화 : z = $\frac{\bar{X} - \mu}{\sigma / \sqrt{n}}$ ~ N(0,1)
-
모 표준편차 $\sigma$ 을 모를때 → 표본 표준편차($s$)를 $\sigma$ 대신 활용 : z = $\frac{\bar{X} - \mu}{s / \sqrt{n}}$ ~ N(0,1)
-
-
n < 30 이고, 모분포가 정규분포일때
-
모 표준편차 $\sigma$ 을 알 때의 표준화 : z = $\frac{\bar{X} - \mu}{\sigma / \sqrt{n}}$ ~ N(0,1)
-
모 표준편차 $\sigma$ 을 모를때 → t분포 활용 : t = $\frac{\bar{X} - \mu}{s / \sqrt{n}}$ ~ Student’$t$ 분포
-
표본비율의 분포
-
분석의 대상이 모집단의 평균이 아니라 비율인 경우
-
예시) 제품의 불량률, 특정 선거후보자에 대한 투표자의 지지율
-
표본비율에 대한 평균 : $p$
-
표본비율에 대한 분산 : $\frac{pq}{n}$
-
조건) np ≥ 5이고 n(1-p)≥ 5 일때
- $N~(p, \frac{p(1-p)}{n})$
Reference
-
- Lind, Marchal, Wathen, (2018), McGrawHill, 강종열 등 역, 지필미디어