Contents
-
모표준편차를 알고 동일할 때, 두개의 독립적인 모평균이 동일하다는 가설검정을 수행한다.
-
모표준편차를 알지 못할 때, 두 개의 독립적인 모평균이 동일하다는 가설검정을 수행한다.
-
쌍세 표본 또는 종속적 표본의 관측자료를 통한 모집단 평균의 차이에 대한 가설검정을 수행한다.
-
독립적인 표본과 종속적인 표본의 차이를 설명한다.
독립표본
-
독립표본: 독립 모집단들로부터 별도로 수집된 표본들- 각 모집단은 다른 모집단에서 일어난 사건에 영향을 받지 않음
-
두 표본을 대상으로 하는 가설 검정: 독립표본
-
두 모집단 비교를 위해서, 두 표본의 차이를 살펴본다.
-
평균에 대한 두 표본검정 $\sigma$ 를 아는 경우
-
$z = \frac{\bar{x_1} - \bar{x_2}}{\sqrt{\frac{\sigma^{2}}{n_1}} + \frac{\sigma^{2}}{n_2}}$
-
가설검정 절차
두 표본을 활용할 경우 가설검정의 단계
-
단계1: 가설의 설정 → 귀무가설 & 대립가설
-
단계2: 유의수준 결정 → $\alpha$ = 0.01 or $\alpha$ = 0.05
-
단계3: 검정통계량 선택 → z or t
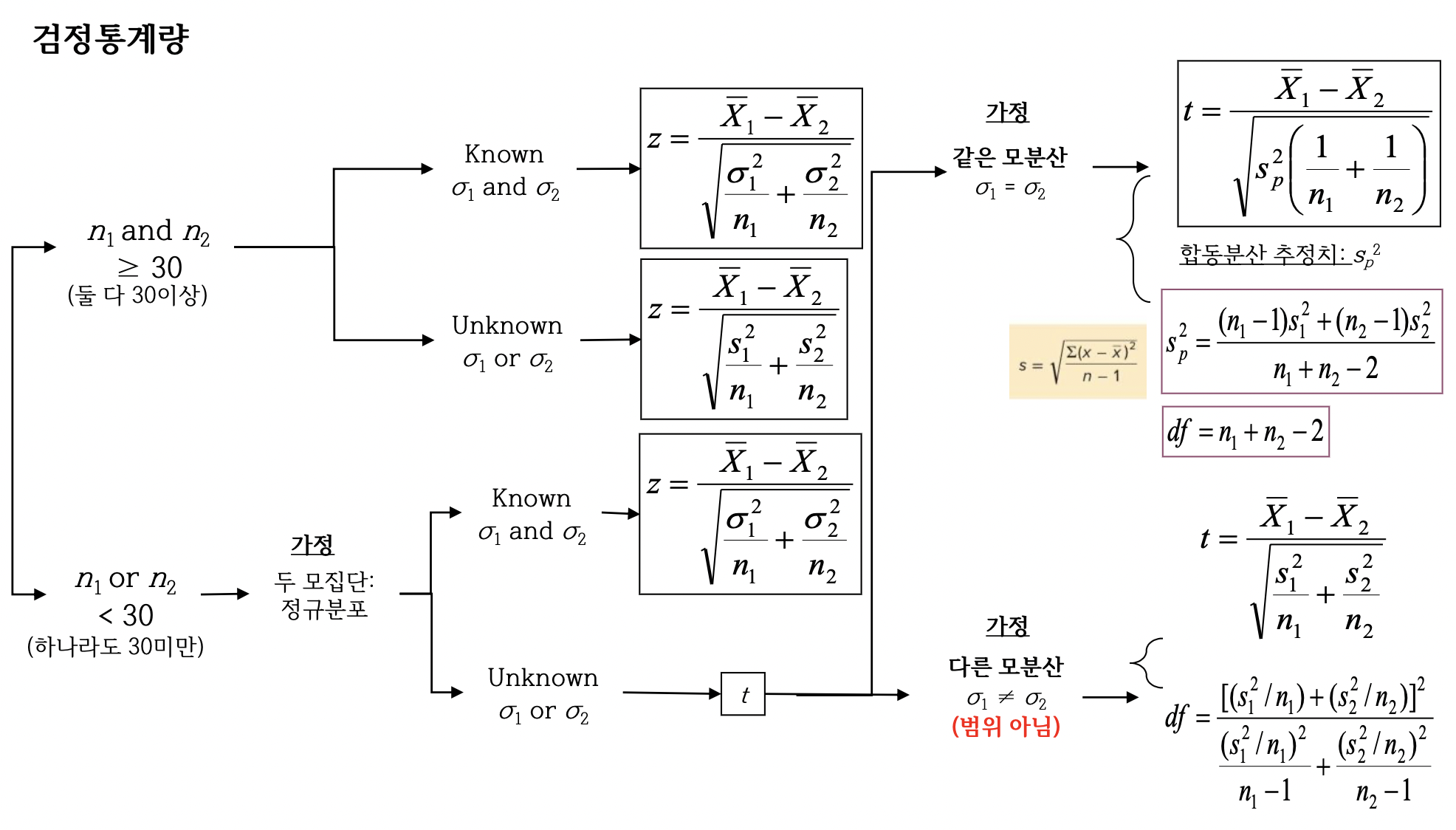
-
단계4: 임계값 및 기각영역 결정 → 기각값: $\alpha$에 해당하는 z값 또는 t값 , 기각영역: 기각값이 결정
-
단계5: 귀무가설의 기각여부 → 검정통계량 계산 후 기각값 또는 기각영역과 비교
종속표본
-
종속표본: 종속된 모집단들로부터 수집된 서로 대응되는 표본들 -
종속표본의 구조: 두 표본의 관측치 간 차이값으로 가설검정을 진행함
-
차이값을 하나의 표본으로 간주하여 가설검정을 진행
-
평균 → $\bar{d} = \frac{\sum d_i}{n}$
-
표준편차 → $s_d = \sqrt \frac{\sum (d_i - \bar{d})^2}{n-1}$
Reference
-
- Lind, Marchal, Wathen, (2018), McGrawHill, 강종열 등 역, 지필미디어