devFancy BE Developer

02. Random Variables

2022-05-03
devfancy
Probability-Statistics

이 글은 컴퓨터학부 확률과통계 수업에서 배운 자료들을 정리한 내용입니다.

Contents

  • 2.1 Discrete Random Variables

  • 2.2 Continuous Random Variables

  • 2.3 The Expectation of a Random Variables

  • 2.4 The Variance of a Random Variables

  • 2.5 Jointly Distributed Random Variables

  • 2.6 Combinations and Functions of Random Variables

2.1.1 Definition of a Random Variable

  • Random Variables : A random variable is obtained by assigning a numerical value(임의로 할당) to each outcome of a particular experiment

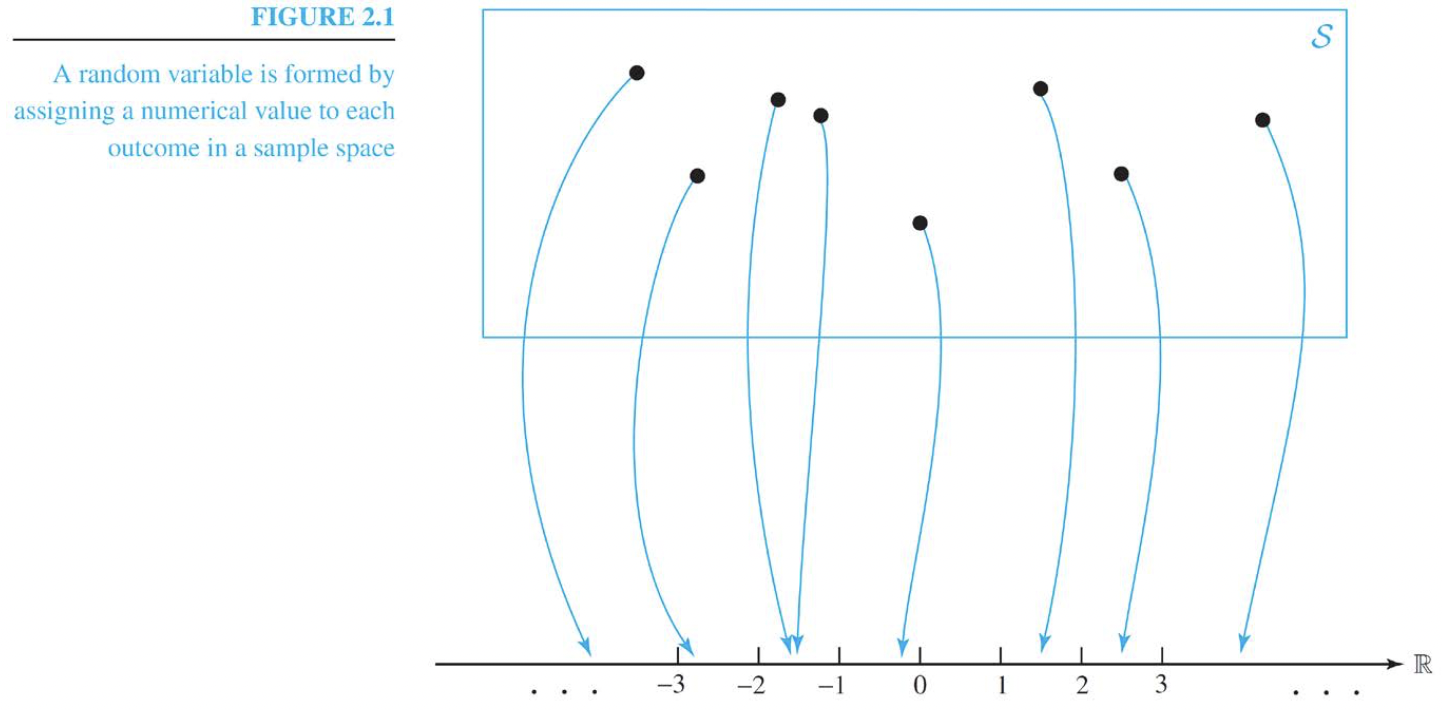
2.1.2 Probability Mass Function

  • Probability Mass Function (p.m.f) ⇒ ~값일 때 확률이 얼마인가 ?

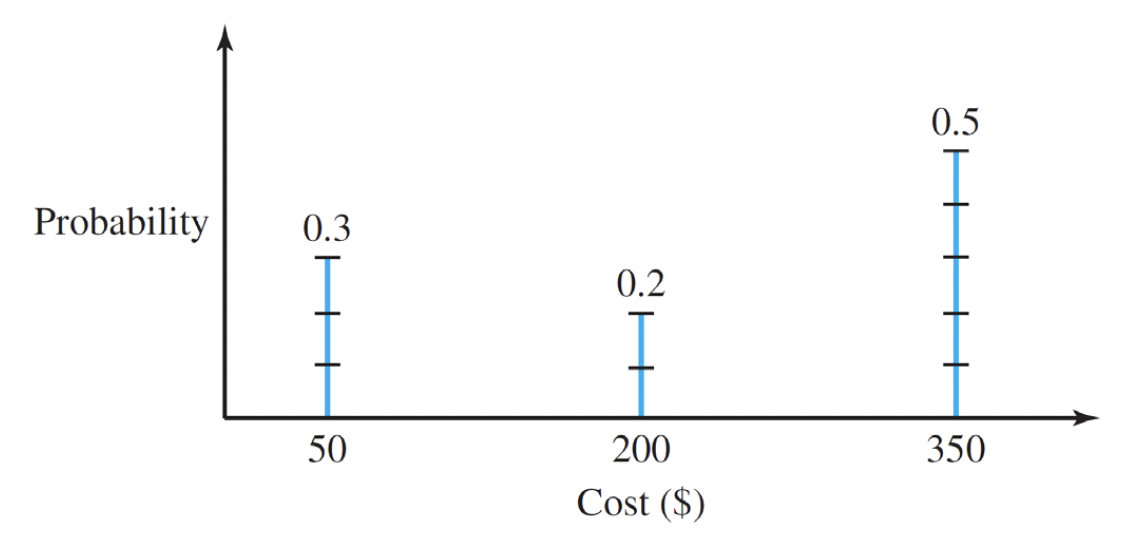
The Probability mass function(p.m.f) of a random variable $X$ is set of probability values $p_i$ assigned to each of the value $x_i$ taken by the $discrete$ random variable.

These probability values must satisfy $0 ≤ p_i ≤ 1$ and $\sum_{i} p_i = 1$ .

The probability that $P(X = x_i) = p_i$

$P(X = x_i)$ ⇒ ex) $P(X = 50)$ 일 확률은 ? 0.3

$X$: 변수

$x_i$ : 값

2.1.3 Cumulative Distribution Function

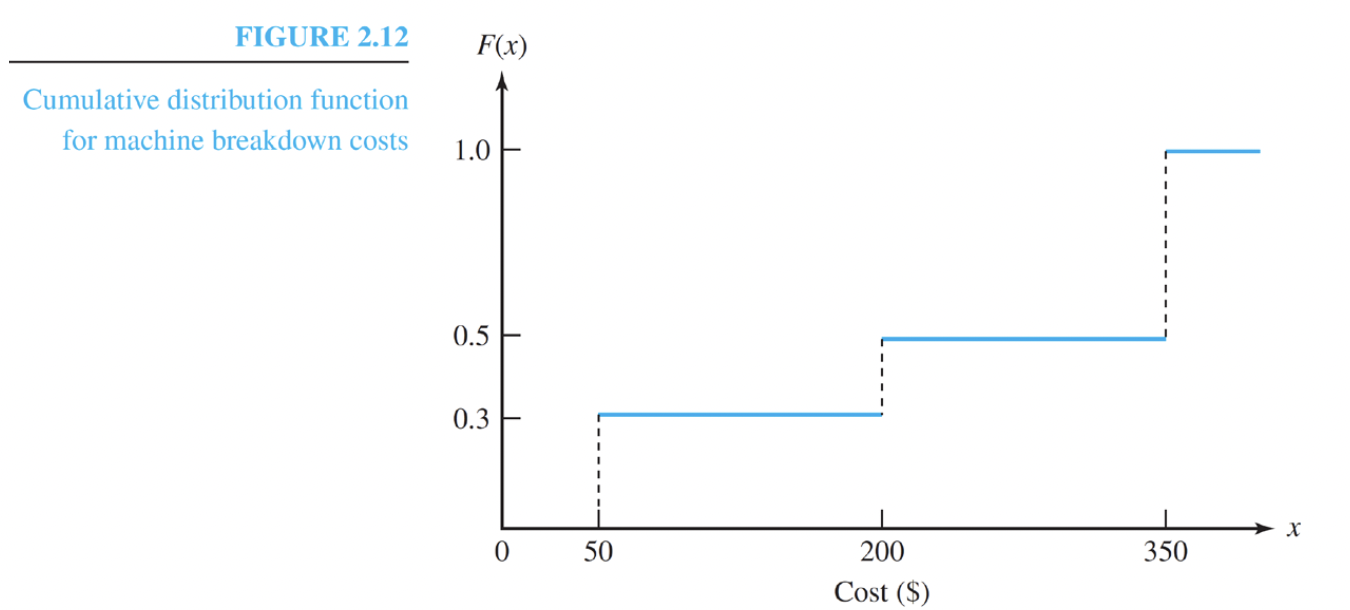
  • Cumulative Distribution Function(c.d.f) - 누적 분포 함수

The cumulative distribution function(c.d.f) of a random variable $X$ is the function

$F(x) = P(X≤x)$

  • 범위에 있는 값들을 누적해서 더한 값.

2.2.2 Probability Density Function

  • Probability Density Function (p.d.f)

A probability density function $f(x)$ defines the probabilistic properties of a continuous random variable. it must satisfy $f(x) ≥ 0$ and

$\int_{state\ space} f(x)\, dx = 1$

The probability that the random variable lies between two values is obtained by integrating the probability density function between the two values.

  • PMF vs PDF 비교

  • X가 가질 수 있는 값이 너무 많다 → Continuous Random Variable

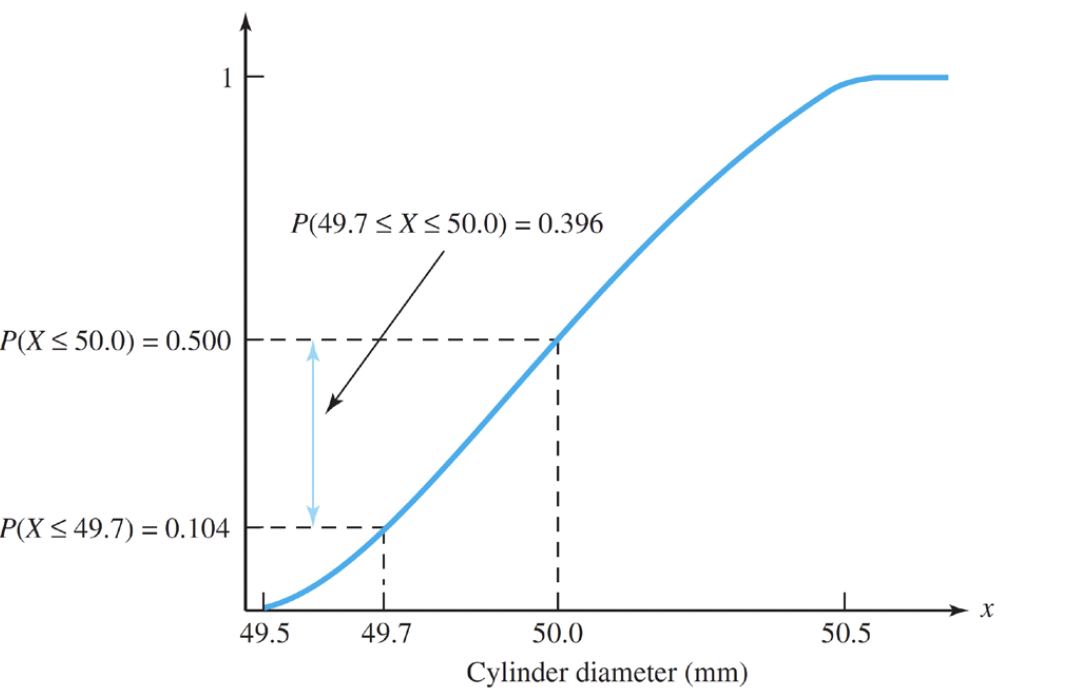
2.2.3 Cumulative Distribution Function

  • Cumulative Distribution Function → 예시)

2.3.1 Expectations of Discrete Random Variables

  • Expectations of Discrete Random Variables

the expected value or expectation of a discrete random variable with a probability mass function $P( X = x_i) = p_i$ is

$E(x) = \Sigma_{i}\ p_i x_i$

E(X) provides a summary measure of the average value taken by the random variable and is also known as the mean of the random variable

2.3.2 Expectations of Continuous Random Variables

  • Expectations of Continuous Random Variables

the expected value or expectation of continuous random variable with a probability density function f(x) is $E(x) = \int_{state\ space} xf(x)\, dx$$E(x) = \int_{state space} xf(x)\, dx$

the expected value provides a summary measure of the average value taken by the random variable, and it is also known as mean of the random variables.

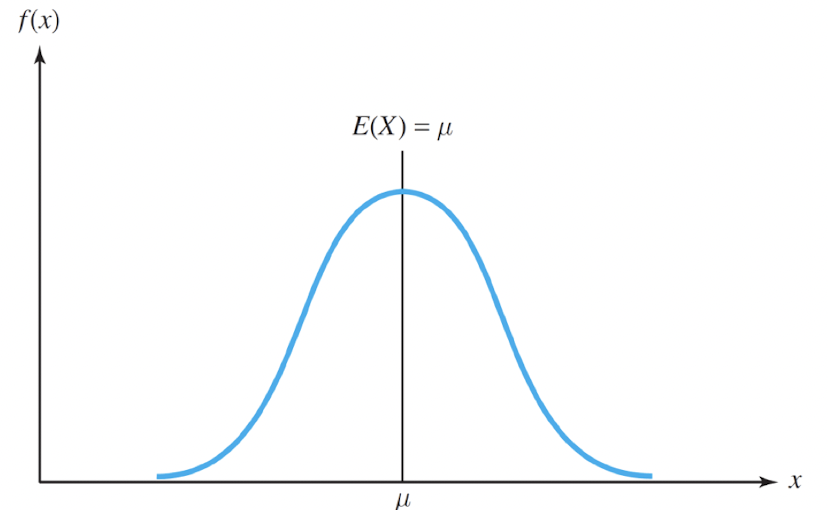
  • Symmetric Random Variables

If a continuous random variable $X$ has a probability density function f(x) that is symmetric about a point $$ $\mu$ so that $f(\mu + x) = f(\mu - x)$ for all $x \in R $ , then $E(X) = \mu$, so that the expectation of the random variable is equal to the point of symmetry.

  • A random variables as a function $g(X)$

    • $E(g(X)) = \sum_{i} p_{i} g(x_{i})$ for a discrete random variable as a function → $p_{i}$ 는 고정

    • $E(g(X)) = \int_{state\ space} f(x)g(x) dx$ for a continuous random variable as a function → $f(x)$는 고정

    • $g(X) = X^{2}, E(g(X)) = E(X^{2})$

2.4.1 Definition and Interpretation of Variance

  • Variance → $\sigma^{2}$

    • $Var(X) = E((X - E(X))^{2})$

    • $Var(X) = E(X^{2}) - ( E(X))^{2}$

    • The Variance is a positive quantity that measures the spread of the distribution of the random variable about its mean value.

  • Standard Deviation → $\sigma$

    • The Standard Deviation of a random variable $X$ is defined to be the positive square root of the variance

2.4.3 Chebyshev’s Inequality

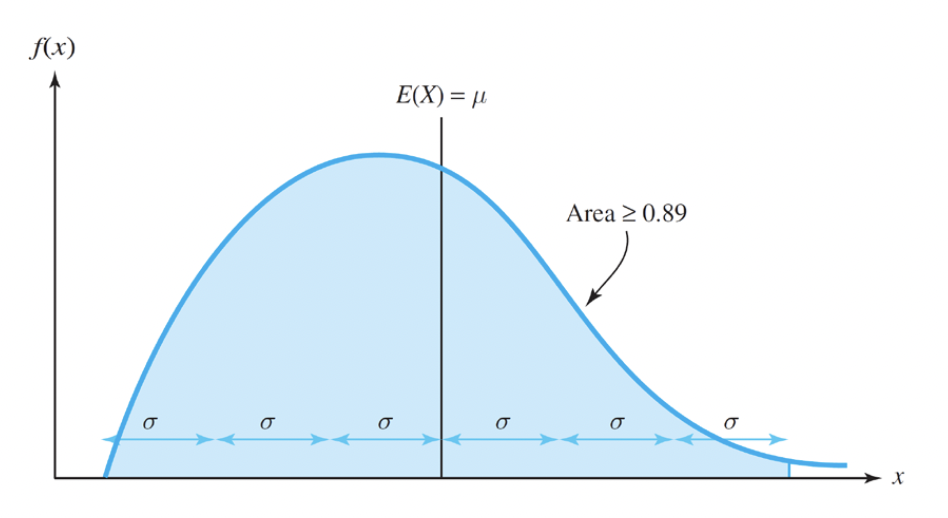
  • Chebyshev’s Inequality

If a random variable has a mean $\mu$ and a variance $\sigma^{2}$, then

$P(\mu - c\sigma ≤ X ≤ \mu + c\sigma ) ≥ 1 - \frac{1}{c^{2}}$

for c ≥ 1

  • for example, taking c = 2 gives $P(\mu - 2\sigma ≤ X ≤ \mu + 2\sigma ) ≥ 1 - \frac{1}{2^{2}} = 0.75$

  • for example, taking c = 3 gives $P(\mu - 3\sigma ≤ X ≤ \mu + 3\sigma ) ≥ 1 - \frac{1}{3^{2}} = 0.89$

2.4.4 Quantiles of Random Variables

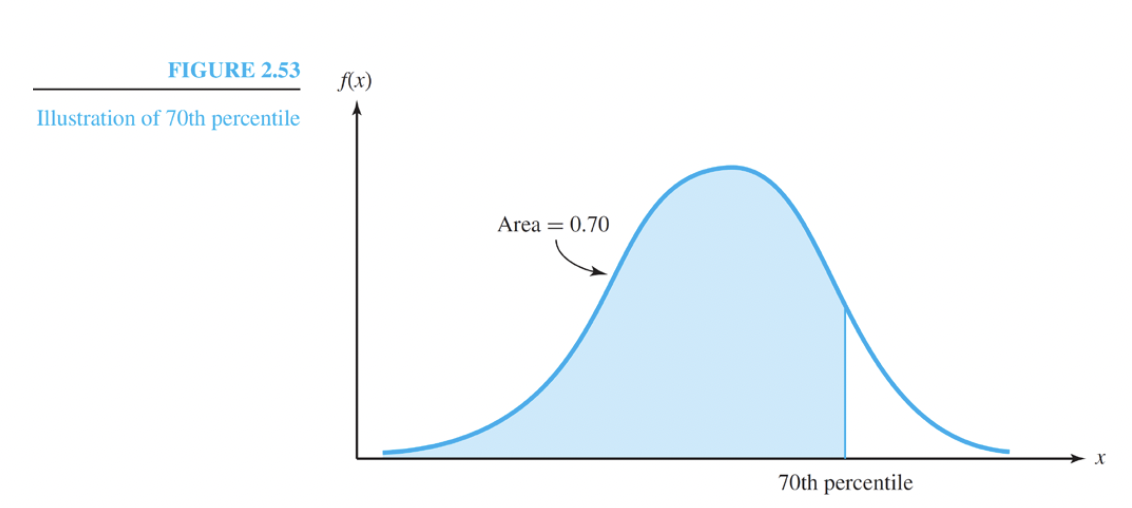
  • Quantiles

The $p$th quantile of a random variable $X$ with a cumulative distribution function $F(x)$ is defined to be the value x for which

$F(x) = p$ → p 는 확률값 ex) 0.7

This is also referred to as the p x 100 th percentile of the random variable.

There is a probability of p that the random variable takes a value less than the pth quantile.

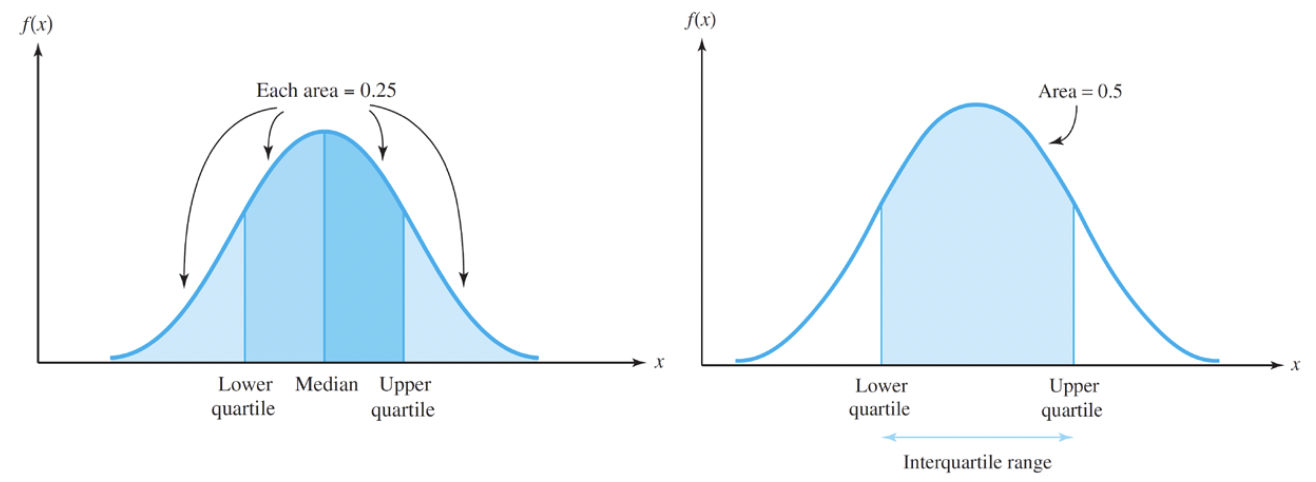
  • Quartiles and Interquartile Range

    • Upper quartile: The 75th percentile of the distribution → 75%에 해당하는 값

    • Lower quartile: The 25th percentile of the distribution → 25%에 해당하는 값

    • Interquartile range: The distance between the two quartiles

2.5.1 Jointly Distributed Random Variables

  • Joint Probability Distributions

  • It is often appropriate to consider two random variables X and Y and their joint probability distribution

  • If the random variables are discrete, then the joint probability mass function (p.m.f) consists of probability values

$P( X = x_{i}, Y = y_{j} ) = p_{ij} ≥ 0$

satisfying $\sum_{i} \sum_{j} p_{ij} = 1$

If the random variables are continuous, then the joint probability density function (p.d.f) is a function

$f(x, y) ≥ 0$ satisfying $\int \int_{state\ space} f(x, y) dxdy = 1$

2.5.2 Marginal Probability Distributions

  • Marginal Probability Distributions → X 또는 Y 둘중 하나만 보는 경우

  • The marginal distribution of a random variable $X$ is obtained from the joint probability distribution of two random variables $X$ and $Y$ by summing or integrating over the values of the random variable $Y$. The marginal distribution is the individual probability distribution of the random variable $X$ considered alone.

  • For two discrete random variables $X$ and $Y$, the probability values of the marginal distribution of $X$ are

$P( X = x_{i} ) = p_{i+} = \sum_{j} p_{ij}$

  • For two continuous random variables, the probability density function of the marginal distribution of $X$ is

$f_{X}(x) = \int_{\infty}^{\infty} f(x, y) dy$

2.5.3 Conditional Probability Distributions

  • Conditional Probability Distributions (조건부 확률)

The conditional distribution of a random variable X conditional on a random variable Y taking a particular value summarizes the probabilistic properties of the random variable X under the knowledge provided by the value of Y. It consists of the probability values

$p_{i Y = y_{j}} = P( X = x_{i} Y = y_{j} ) = \frac{P( X = x_{i}, Y = y_{j})}{P( Y = y_{j})} = \frac{p_{ij}}{p_{+j}}$

for discrete random variables or the probability density function

$f_{X Y = y} (x) = \frac{f(x, y)}{f_{Y}(y)}$

for continuous random variables, where $f_{Y}(y)$ is the marginal distribution of the random variable $Y$.

2.6.1 Linear Functions of a Random Variable

  • Linear Functions of a Random Variable

If $X$ is a random variables and $Y = aX + b$ for some numbers $a, b \in R$, then

$E(Y) = aE(X) + b$

and

$Var(Y) = a^{2}Var(X)$

2.6.2 Linear Combinations of Random Variables

  • Sums of Random Variables

    • The expectation of two random variables $X_{1}$ and $X_{2}$

      • $E( X_{1} + X_{2} ) = E( X_{1} ) + E( X_{2} )$

    • The variance of two random variables $X_{1}$ and $X_{2}$

      • $Var( X_{1} + X_{2} ) = Var( X_{1} ) + Var( X_{2} ) + 2Cov(X_{1}X_{2})$

      • Two independent random variables

        • $Var( X_{1} + X_{2} ) = Var( X_{1} ) + Var( X_{2} )$

  • Averaging Independent Random Variables

    • $\bar{X} = \frac{X_{1} + . . . + X_{n}}{n}$

    • $E( \bar{X} ) = \mu$

    • $Var( \bar{X} ) = \frac{\sigma^{2}}{n}$

Reference

Back : 01. Probability Theory

Next : 03. Discrete Probability Distributions

Comments

Index