지금의 기록이 미래의 자산이 된다.
Today's records become tomorrow's assets.-
쿠키와 세션
쿠키를 사용하게 된 배경
-
HTTP 주요 특징은 무상태성과, 비연결성이다.
-
무상태성은 서버가 클라이언트의 상태를 보존하지 않는다는 것을 의미하고,비연결성은 말 그대로 연결을 유지하지 않는다는 것을 의미한다. -
두가지 특징에 대한 자세한 설명은 HTTP 기본에 작성해두었다.
-
예를 들어, 홈페이지에서 로그인을 하고 난 뒤에 새로 고침을 하게 되면 로그인이 풀리는 상태가 된다.
-
로그인을 유지하기 위해서 서버가 다수의 클라이언트와 연결을 유지할 수 있지만, 그로 인해 자원이 낭비가 된다.
-
이러한 HTTP의 2가지 특징을 보완하기 위해
쿠키가 등장하게 되었다.
쿠키(Cookie)
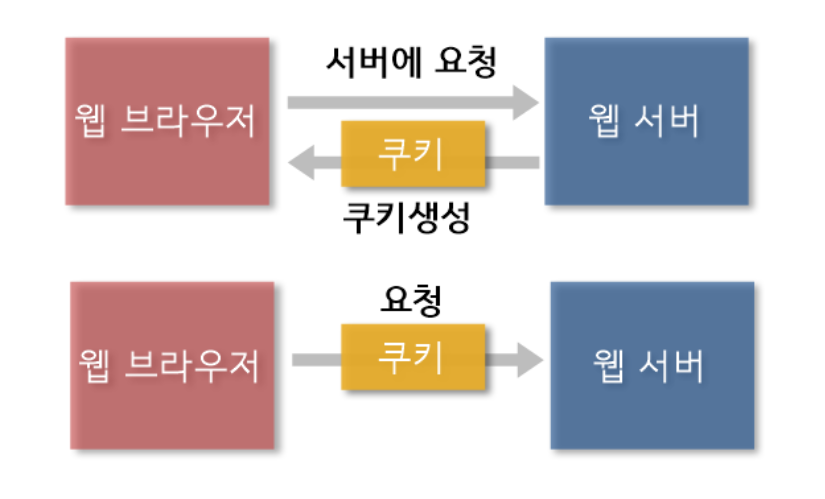
쿠키(Cookie)는 사용자(클라이언트)가 어떤 웹 사이트를 방문할 때, 사용자의 웹 브라우저를 통해 사용자 로컬에 키(Key)와 값(Value) 을 저장하는 작은 데이터 파일이다.
-
서버는 클라이언트의 로그인 요청에 대한 응답을 작성할 때, 클라이언트 측에 저장하고 싶은 정보를 응답 헤더의
Set-Cookie에 담아 전달한다. -
이후 해당 클라이언트는 요청을 보낼 때마다 요청 헤더에
Cookie를 담아 전송한다. -
쿠키에 담긴 정보를 통해 서버는 해당 요청의 클라이언트가 누구인지 식별한다.
쿠키의 타입
-
쿠키는
세션 쿠키와지속 쿠키, 두 가지 타입으로 나뉜다. -
세션 쿠키(Session Cookie) : 브라우저 메모리에 저장되므로, 사용자가 사이트를 검색할 때 관련된 설정과 선호 사항들을 저장하는 임시 쿠키로 브라우저를 종료하면 해당정보가 삭제된다. -
지속 쿠키(Persistent Cookie) : 파일로 저장되므로, 브라우저가 종료되거나 컴퓨터가 재시작되어도 해당정보가 남아있다. -
두 가지 쿠키를 구분하는 기준은 파기되는 시점이다. 파기되는 시점을 가리키는
Expires혹은Max-Age파라미터가 없으면 세션 쿠키이다.
Set-Cookie: <쿠키 이름>=<쿠키 값>; Expires=종료 시점 Set-Cookie: <쿠키 이름>=<쿠키 값>; Max-Age=유효 기간쿠키의 단점
쿠키가 브라우저, 즉 클라이언트 측에 저장된다라는 것은 상당히 널리 알려진 사실이다. 이 부분은 쿠키가 탄생하게 된 중요한 배경이며, 안타깝게도 갖가지 이슈가 존재한다.
따라서 쿠키를 사용할 때는 아래와 같은 쿠키의 한계점들을 잘 인지하고 사용하는 것이 중요하다.
-
쿠키의 값이 브라우저에서 확인할 수 있어서 누군가로부터 유출 및 조작 당할 위험이 존재하므로 보안에 취약하다.
-
쿠키는 작은 데이터 파일로, 용량에 제한이 있기 때문에 많은 정보를 담을 수 없다.
-
웹 브라우저마다 쿠기에 대한 지원 형식이 다르기 때문에 브라우저 간에 공유가 불가능하다.
-
쿠기의 사이즈가 커질수록 네트워크에 부하가 심해진다.
쿠키의 보안 속성
이러한 쿠키의 한계와 대체 기술에도 불구하고 반드시 쿠키를 사용해야 하는 상황이라면 가급적 보안 속성을 사용하시기를 권장한다.
- 첫번째 보안 속성은
Secure이다.Set-Cookie응답 헤더에 이 속성이 명시된 쿠키는 브라우저가https프로토콜 상에서만 서버로 돌려 보낸다. 네트워크 상에서 탈취되었을 때 문제가 될 수 있는 쿠키를 상대로 쓰면 유용할 것이다.
Set-Cookie: <쿠키 이름>=<쿠키 값>; Secure- 두번째 보안 속성은
HttpOnly이다.Set-Cookie응답 헤더에 이 속성이 명시된 쿠키는 이 속성이 명시된 쿠키는 브라우저에서 자바스크립트로Document.cookie객체를 통해 접근할 수 없다.
Set-Cookie: <쿠키 이름>=<쿠키 값>; HttpOnly세션(Session)
-
쿠키는 브라우저에 저장하기 때문에 보안에 취약하는 단점이 있다.
-
쿠키의 가장 큰 단점인 유출 및 조작 당할 위험을 보완하기 위해
세션을 사용한다. -
세션은 비밀번호와 같은 클라이언트의 인증 정보를 쿠키가 아닌 서버에 저장하고 관리한다.
-
클라이언트가 서버측에 요청을 보내면, 해당 서버의 엔진이 클라이언트에게 유일한 ID를 부여하는데, 이때 이 유일한 ID가
세션ID이다.
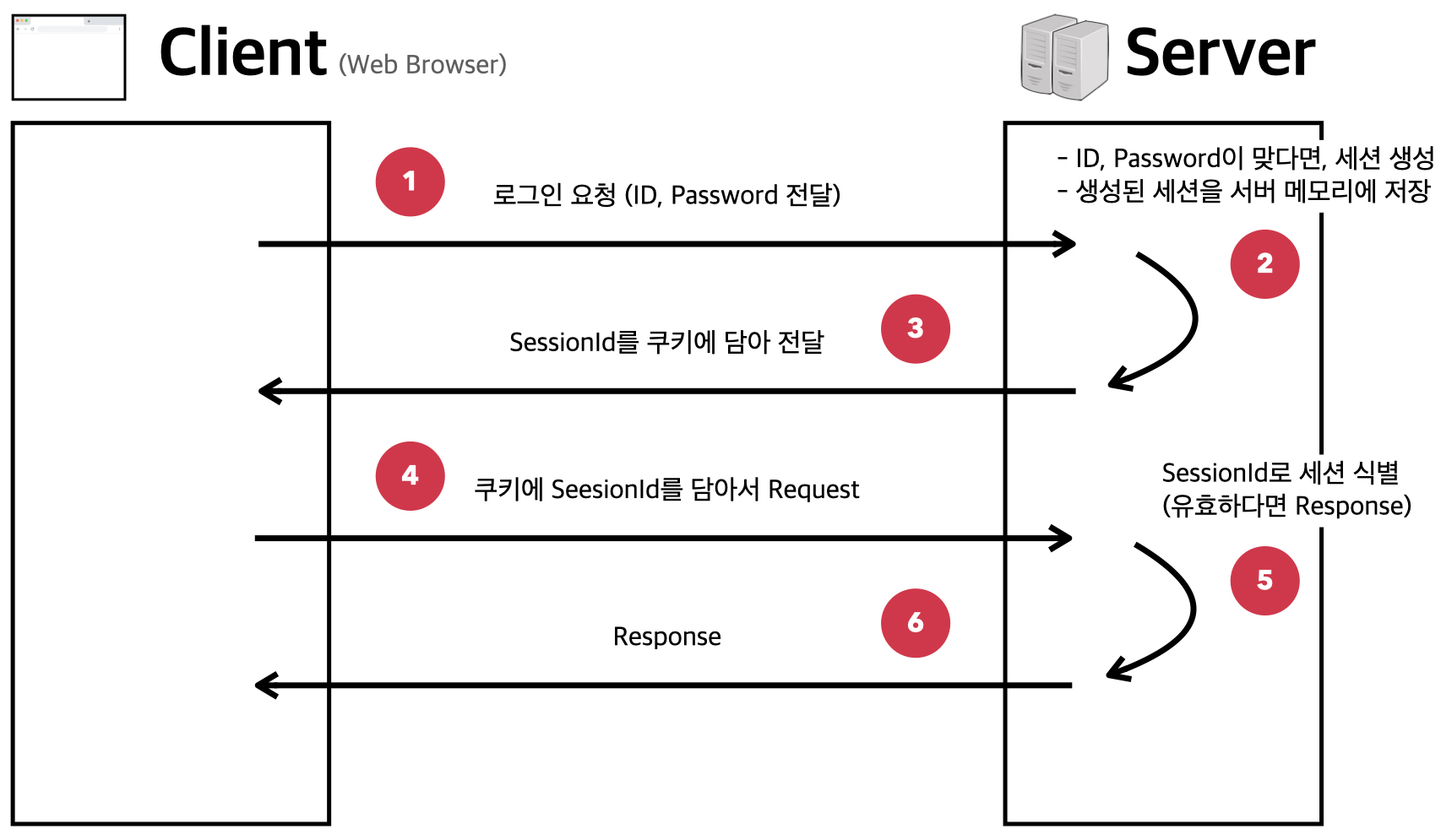
- 클라이언트가 서버에게 로그인 요청(ID, Password)을 보낸다.
- 서버는 로그인 요청이 정상적으로 처리된다면, 유일한 ID인
세션ID을 생성하여 서버의 메모리에 저장한다. - 서버가 클라이언트의 로그인 요청에 대한 응답을 보낼 때 이전에 생성한
세션ID를 쿠키에 담아서 전달한다. - 이후에 클라이언트는 요청을 보낼 때마다 쿠키에 있는
세션ID를 전달한다. - 서버는
세션ID의 유효성을 판별하여 클라이언트를 식별한다. - 사용자가 브라우저를 종료하면 Session의 정보는 삭제된다.
세션의 장단점
-
장점1 : 쿠키를 포함한 요청이 외부에 노출되더라도 세션ID 자체는 유의미한 개인정보를 담고 있지 않아서 비교적 안전하다.
-
단점1 : 하지만 누군가가 중간에 세션ID를 탈취해서 클라이언트인척 위장할 수 있다는 한계는 존재한다.
-
장점2 : 각 사용자마다 유일한 ID인 세션ID가 발급되므로, 요청이 들어올 때마다 회원 정보를 확인할 필요가 없다.
-
단점2 : 클라이언트의 인증 정보가 서버에 메모리에 저장되므로 클라이언트의 요청이 많아지면 서버에 부하가 심해진다.
쿠키와 세션의 차이
쿠키 세션 저장위치 쿠키는 브라우저에 메모리 또는 파일로 저장된다 세션은 서버의 메모리에 저장된다 보안 쿠키는 브라우저에서 확인할 수 있으므로 유출 및 조작 당할 위험이 존재한다 세션은 클라이언트 정보가 서버의 메모리에 저장되므로 비교적 안전하다 라이프 사이클 쿠키는 파일로 저장될 때 브라우저가 종료되어도 정보가 남아있다 세션은 서버의 만료시간/날짜가 지나면 사라지거나 브라우저 종료시 세션ID가 사라진다 속도 쿠키에 정보가 있기 때문에 서버에 요청시 속도가 빠르다 세션은 서버의 메모리로부터 세션ID를 조회해야 하므로 속도가 쿠키보다 비교적 느리다 세션을 주로 사용하면 좋은데, 왜 굳이 쿠키를 사용하는 이유는?
세션은 브라우저가 아닌 서버에 데이터를 저장하므로, 서버의 메모리를 계속 사용하면 속도 저하가 올 수 있기 때문이다.
웹 개발에서 쿠키를 사용할 수 밖에 없는 결정적인 이유
HTTP 프로토콜은 서버가 클라이언트의 상태를 보존하지 않는 무상태성과 연결을 유지시키지 않는 비연결성 특징을 가지고 있다.
즉, 서버가 클라이언트의 요청에 응답을 하는 순간 HTTP 연결은 끊어지며, 클라이언트에서 새로운 요청을 해야 다시 HTTP 연결이 맺어지게 된다.
간단한 웹사이트가 아닌 이상 대부분의 서비스에서는 하나의 브라우저로 부터 순차적으로 들어오는 여러 개의 요청이 동일한 사용자로 부터 오는 것이라는 것을 알아야 한다.
클라이언트와 연결이 유지되지 않는 상황에서 동시에 서버로 유입되는 수많은 요청이 각각 어느 사용자의 것인지 판단하는 것은 서버 입장에서 매우 힘든 일이다.
여기서 쿠키의 지속성이 빛을 발휘하게 된다.
바로 서버가 쿠키를 한 번 브라우저에 저장하면 브라우저는 해당 쿠키를 매 요청마다 계속해서 서버로 돌려 보낸다는 것이다. 다시 말해 서버가 브라우저에 쿠키 하나만 심어 놓으면 그 후로 브라우저는 성실하게 매번 서버를 방문할 때 마다 해당 쿠키를 다시 가져온다.
이러한 쿠키의 특성을 활용하면 서버는 각 요청이 어느 브라우저에서 오는 것인지 어렵지 않게 판단할 수 있다.
예를 들어, 사용자가 서비스에 최초로 접속했을 때 서버가 브라우저에게
a=1쿠키를 저장하라고 시키면,HTTP 요청
GET /index.html HTTP/1.1 Host: www.test.comHTTP 응답
HTTP/1.1 200 OK Content-Type: text/html Set-Cookie: a=1해당 브라우저는 사용자가
www.test.com이라는 도메인에 머무는 한/index.html을 방문하든/about.html을 방문하든/contact.html을 방문하든 매번 같은 쿠키를 돌려준다.그러므로 서버 입장에서는
a=1쿠키를 들고 들어오는 요청은 모두 이 브라우저로 부터 오는 것이구나라고 쉽게 알 수 있다.(물론 다른 브라우저에게
a=1대신에a=2,a=3와 같은 다른 쿠키를 응답해줘야 한다)쿠키와 캐시의 차이
-
쿠키는 사용자를 식별하고 세션을 유지하는 방식 중에서 현재까지 널리 사용하는 방식이다.
-
쿠키는 캐시와 충돌할 우려가 있으므로 대부분의 캐시나 브라우저는 쿠키에 있는 정보를 캐싱하지 않는다.
쿠키 캐시 정의 쿠키는 정보를 저장하기 위해 사용된다. 기본적으로 웹서버에서 PC로 보내는 작은 파일들을 저장한다. 보통 쿠키는 누군가 특정한 웹 사이트를 접속할 때 발생한다. 캐시 또한 웹 페이지 요소를 저장하기 위한 임시 저장소이다. 특히, 나중에 필요할 것 같은 요소들을 저장한다.이러한 요소들은 그림 파일이나 문서 파일 등이 될 수 있다. 목적 쿠키는 사용자의 인증을 도와준다. 캐시는 웹 페이지가 빠르게 렌더링 할 수 있도록 도와준다. 삭제 쿠키는 만료기간이 있어 시간이 지나면 자동삭제 된다. 캐시는 사용자가 직접 수동으로 삭제해주어야한다. 예시 유저의 선호도(로그인 정보, 방문기록, 방문횟수) 오디오, 비디오 파일
-
-
[Programmers] 155651. 호텔 대실(누적합)
성능 요약
- 메모리: 79.2 MB, 시간: 3.52 ms
구분
- 코딩테스트 연습 > 연습문제 > 호텔 대실(누적합)
Answer Code1(23.10.24)
```java import java.util.*;
-
[Programmers] 131704. 택배상자
성능 요약
- 메모리: 123 MB, 시간: 33.14 ms
구분
- 코딩테스트 연습 > 스택, 구현
Answer Code1(23.10.23)
import java.util.*; /** * main_con : 메인 컨테이너 * sub_con : 서브 컨테이너 * 주문 갯수만큼 for 문 돌리면서 * 1) 현재 순서와 맞는 택배 상자가 올때까지 서브 컨테이너 벨트에 저장한다. * 1-1) 메인 컨테이너의 현재 위치에 있는 값과 일치하면 break; * 1-2) 서브 컨테이너가 비어있지 않고, 서브 컨테이너의 현재 위치에 있는 값과 일치하면 break; * 1-3) 메인, 서브에 있는 값과 일치하지 않으면 1 증가시켜 1-1로 되돌아간다. * 2) 서브 컨테이너(Stack)에 다 저장되었으면 탐색 시작한다. * 2-1) 메인 컨테이너의 현재 위치에 있는 값과 일치하면 정답 갯수 +1 증가 * 2-2) 서브 컨테이너가 비어있지 않고, 서브 컨테이너의 현재 위치에 있는 값과 일치하면 서브 컨테이너 pop()하고 정답 갯수 + 1 증가 * 2-3) 메인, 서브에 있는 값과 일치하지 않으면 종료 */ class Solution { public int solution(int[] order) { int answer = 0; int main_con = 1; Stack<Integer> sub_con = new Stack<>(); for(int o : order) { while(main_con <= order.length) { // 1 if(main_con == o) break; // 1-1 else if(!sub_con.isEmpty() && sub_con.peek() == o) // 1-2 break; else { // 1-3 sub_con.push(main_con); main_con++; } } // 2 if(main_con == o) { // 2-1 answer++; main_con++; } else if(!sub_con.isEmpty() && sub_con.peek() == o) // 2-2 { sub_con.pop(); answer++; } else // 2-3 { break; } } return answer; } }문제 풀이
-
해당 문제는 두개의 컨테이너 벨트가 존재한다.
-
메인 컨테이너는 택배박스를 트럭에 싣기 전에 1부터 n까지 순서대로 놓여져 있는 메인 컨테이너 벨트이고,
-
서브 컨테이너는 순서에 맞지 않는 택배박스를 임시로 놓는 서브 컨테이너 벨드이다.
-
해당 문제에서 우리는 주어진 순서에 해당하는 택배 박스를 메인 또는 서브 컨테이너 벨트에 있는지 확인하고, 이것을 트럭에 싣는 것이다.
-
만약에 메인 컨테이너에 없다면 -> 서브 컨테이너 벨트의 맨 앞의 상자를 확인하고 -> 서브 컨테이너에도 없다면 택배 상자를 서브 컨테이너 벨트에 보관하고, 메인 컨테이너 벨트에서 다음 택배 상자를 확인한다.
할 일을 정리해보면 다음과 같다.
- 정해진 순서에 따른 택배 박스를 확인한다. -> 반복문 이용
- 메인 컨테이너에 있는 상자가 현재 배달하는 순서와 같으면 트럭에 실고
- 그게 아니라면, 서브 컨테이너에 있는 상자를 확인한다.
- 서브 컨테이너에 있는 상자가 현재 배달하는 순서와 같으면 트럭에 실고
- 그게 아니라면, 다음 택배 상자를 확인한다.
- 만약 메인 컨테이너와 서브 컨테이너 벨트의 맨 앞에 있는 상자와 순서가 다르면 종료한다.
Review
- 문제를 이해하는데 시간을 오래 잡아먹었지만, 이해하기에는 크게 어려움이 없었다.
- 다만, 반복문을 어딴 기준을 세우고 해야 할지 감을 잡기 어려웠고, 그래서 그림을 그려서 이해하도록 노력했다.
- 스택의 문법과 구현에 대한 과정을 알 수 있어서 좋은 문제라고 생각한다.
Reference
-
알고리즘/코딩테스트를 위한 코드 정리
Prologue
-
Java로 알고리즘/코딩테스트에서 자주 쓰이는 문법들을 정리하기 위한 포스팅이다.
-
(2025.07.26) 최근에 LeetCode로 문제를 풀면서 새롭게 알게된 개념 및 내용들을 추가했다.
구현
-
구현은 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정이다.
-
Problem -> Thinking -> Solution
-
구현 유형의 예시는 다음과 같다.
-
알고리즘은 간단한데 코드가 지나칠 만큼 길어지는 문제
-
실수 연산을 다루고, 특정 소수점 자리까지 출력해야 하는 문제
-
문자열을 특정한 기준에 따라서 끊어 처리해야 하는 문제
-
적절한 라이브러리를 찾아서 사용해야 하는 문제
-
-
-
구현 유형은
완전 탐색,시뮬레이션을 포함한다.완전 탐색(Brute Forcing) : 모든 경우의 수를 주저 없이 다 계산하는 해결 방법시뮬레이션: 문제에서 제시한 알고리즘을 한 단계씩 차례대로 직접 수행
관련 문제
DFS/BFS
- 깊이 우선 탐색과 너비 우선 탐색은 기본적인 그래프 기법 : DFS, BFS에 정리했으니, 해당 글을 참고하자.
유형1. 연결된 요소 찾기
-
연결된 노드의 개수는 몇 개인가요?
-
연결된 묶음/덩어리의 개수는 몇 개인가요?
-
1번과 연결된 노드의 번호를 오름차순으로 출력하세요
-
1번과 3번의 거리는 얼마인가요?
이 유형을 잘 풀기 위해 고민할 것들
-
주요 키워드: 정점(node), 간선(edge), 연결, 네트워크, 그래프
-
주어진 정보를 어떻게 변환할지 -> 2차원 배열(1,000이하) / ArrayList(1,000 초과)
-
재방문을 방지하는 방법
관련 문제
유형2. 같은 부류 찾기
-
연결된 묶음/덩어리의 개수는 몇 개인가요?
-
가장 큰 덩어리의 크기는 얼마인가요?
이 유형을 잘 풀기 위해 고민할 것들
-
주요 키워드: 인접한 위치로 이동, 상하좌우, 가로/세로, 대각선으로 이동
-
주어진 정보를 어떻게 변환할지
-
재방문을 방지하는 방법
-
어느 지점에서 DFS를 시작할지
-
어느 방향으로 DFS를 진행할지
그외
Stack
-
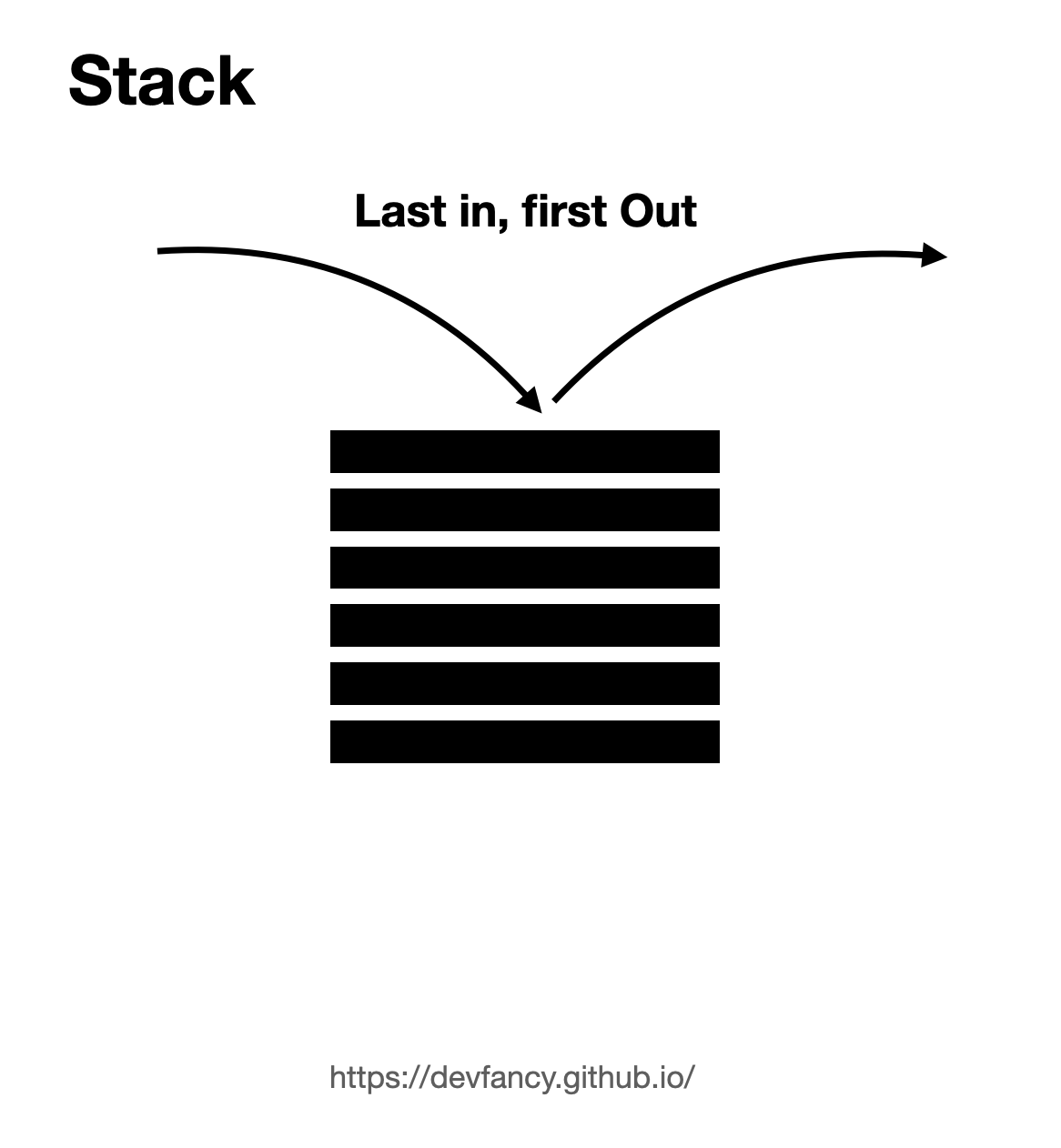
스택은
LIFO(List In First Out, 후입선출) 구조로 데이터를 쌓아올린 형태의 자료구조를 뜻한다. ex) 쓰레기통, 마트용 음료수 진열대, 프링X스(과자) -
즉 한쪽 끝에서만 자료(데이터)를 넣고 뺄 수 있는 형식의 자료 구조이다.
-
스택은 데이터를 쌓는 형식으로 저장하는데 따라서 조회, 추가, 삭제 모두 가장 위에 있는, 가장 최근의 값에서 이루어진다.
-
스택 구조에서 가장 상단에 있는 데이터를
Top라 부른다.
2025.07.26 업데이트
Stack클래스 대신Deque인터페이스를 사용하는 것을 권장한다.-
Java에서
Stack클래스는 오래된Vector클래스를 상속받아 만들어져 지금은 사용이 권장되지 않는다. -
대신,
Deque(데크) 인터페이스와 그 구현체인ArrayDeque를 사용하면 스택의 모든 기능을 더 빠르고 효율적으로 사용할 수 있다.
-
-
실전! 스프링 부트와 JPA 활용2: API 개발 고급 - 컬렉션 조회 최적화 (엔티티 조회 기준)
이 글의 코드와 정보들은 [실전! 스프링 부트와 JPA 활용 2] 강의를 들으며 정리한 내용을 토대로 작성하였습니다.
API 개발 고급
이번 글은
주문내역에서 주문한상품 정보를 추가로 조회하자.Order 기준으로 컬렉션인
OrderItem와Item이 필요하다.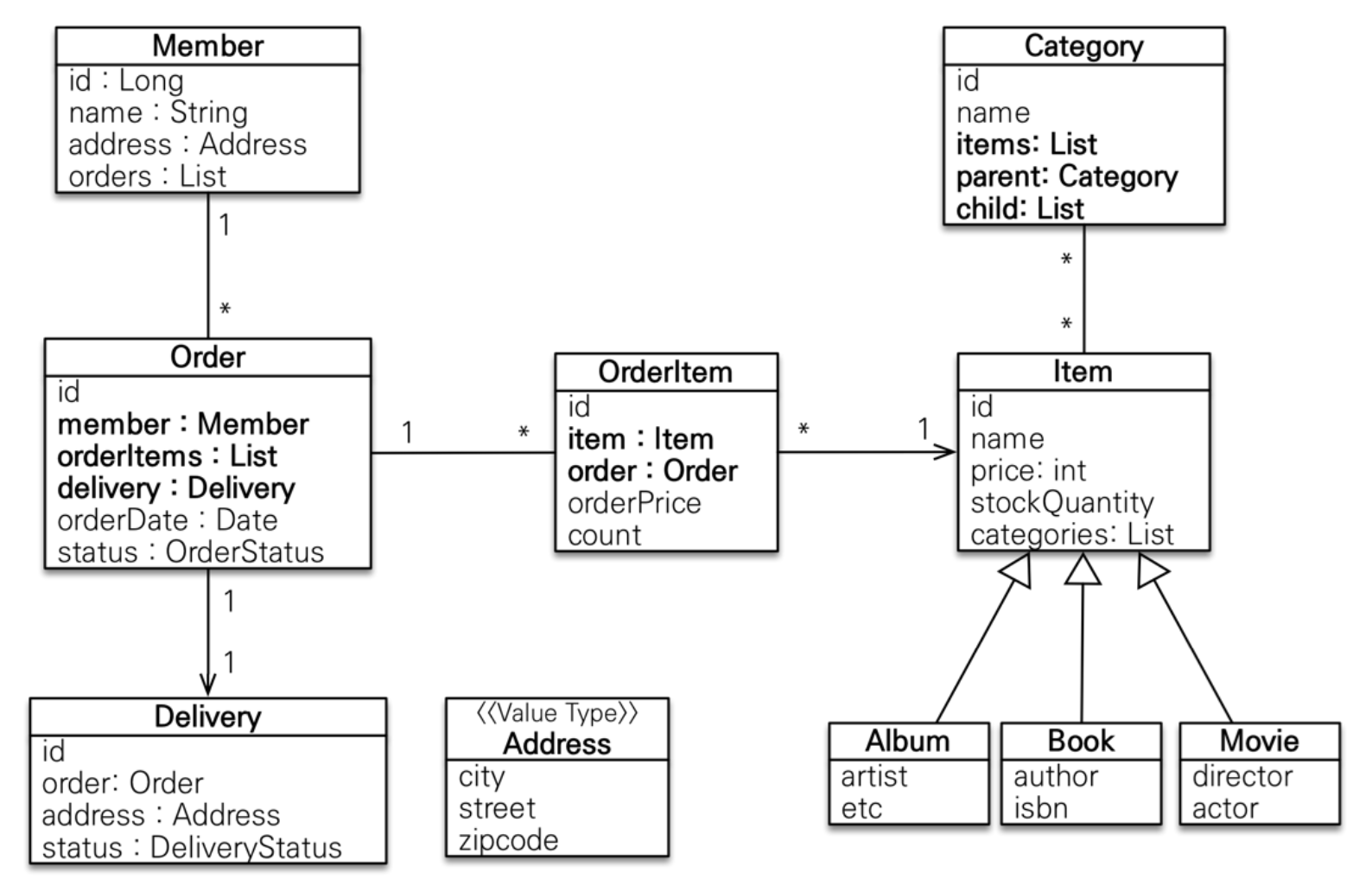
(참고로, 위의 엔티티 테이블에서 확인할 수 있듯이 주문과 주문상품(OrderItem)은 일대다 관계이며, 주문상품과 상품(Item)은 다대일 관계로 구성되어 있다)
이전 글인 지연 로딩과 조회 성능 최적화 부분에서는 toOne(OneToOne, ManyToOne) 관계에 대한 해결책을 정리했다.
이번에는 컬렉션인
엔티티 조회를 기준으로 일대다(OneToMany) 관계를 조회하고, 최적화하는 방법을 알아보자.앞서, 이번 글에서는 V1(엔티티 직접 노출), V2(엔티티를 조회해서 DTO로 변환)은 이전 글에서 이미 다루었기 때문에 생략했다.
주문 조회 V3: 엔티티를 DTO로 변환 - 페치 조인 최적화
OrderApiController에 추가
@RestController @RequiredArgsConstructor public class OrderApiController { @GetMapping("/api/v3/orders") public List<OrderDto> ordersV3() { List<Order> orders = orderRepository.findAllWithItem(); for (Order order : orders) { System.out.println("order ref=" + order + " id=" + order.getId()); } List<OrderDto> result = orders.stream() .map(o -> new OrderDto(o)) .collect(toList()); return result; } }출력결과
order ref=jpabook.jpashop.domain.Order@27dc3bfe id=4 order ref=jpabook.jpashop.domain.Order@27dc3bfe id=4 order ref=jpabook.jpashop.domain.Order@300b5fd6 id=11 order ref=jpabook.jpashop.domain.Order@300b5fd6 id=11-
DB 참조값, JPA pk id 값이 동일하게 2번 반복되어 출력되는 것을 확인할 수 있다.
-
동일하게 반복된 부분을 제거하기 위해 DB 쿼리문에서
distinct를 추가해주면 된다.
OrderRepository에 추가
@Repository @RequiredArgsConstructor public class OrderRepository { private final EntityManager em; public List<Order> findAllWithItem() { return em.createQuery( "select distinct o from Order o" + " join fetch o.member m" + " join fetch o.delivery d" + " join fetch o.orderItems oi" + " join fetch oi.item i", Order.class) .setFirstResult(1) .setMaxResults(100) .getResultList(); } }-
페치 조인(fetch join)으로 SQL이 1번만 실행된다.
-
현재 Order(주문)과 OrderItem(주문상품)의 관계는 일대다 관계이면서 조인이 있으므로 데이터베이스의 row가 증가한다.
-
그 결과 같은 order 엔티티의 조회 수도 증가하게 된다.
-
이런 반복된 부분을 제거하기 위해 SQL에
distinct를 추가하고, 더해서 같은 엔티티가 조회되면, 애플리케이션에서 중복을 걸러주게 된다. -
위의 예시처럼
order가 컬렉션 페치 조인 때문에 중복 조회 되는 것을 막아준다. -
하지만 이런 경우 단점이 존재한다.
-
컬렉션 페치 조인을 사용하면 페이징이 불가능하다.
-
하이버네이트는 경고 로그를 남기면서 모든 데이터를 DB에서 읽어오고, 메모리에서 페이징 해버려 매우 위험한 결과를 초래한다.
-
-
컬렉션 페치 조인은 1개만 사용할 수 있다. 컬렉션 둘 이상에 페치 조인을 사용하게 되면 데이터가 부정합하게 조회 될 수 있기 때문에 사용해선 안된다.
(자세한 내용은 자바 ORM 표준 JPA 프로그래밍을 참고하자)
주문 조회 V3.1: 엔티티를 DTO로 변환 - 페이징과 한계 돌파
그렇다면
페이징 + 컬렉션 엔티티를 함께 조회하려면 어떻게 해야할까?페이징 문제 해결 방안
-
먼저 ToOne(OneToOne, ManyToOne) 관계를 모두 페치 조인한다.
-
ToOne관계는 row 수를 증가시키지 않으므로 페이징 쿼리에 영향을 주지 않는다. -
켈력선은 지연 로딩으로 조회한다.
-
지연 로딩 성능 최적화를 위해 다음 2가지를 중 1개를 사용하면 된다.
-
[1] 글로벌 설정: application.yml 파일에
hibernate.default_batch_fetch_size를 추가한다. -
[2] 개별 최적화: 적용할 엔티티 클래스, 컬렉션 필드 위에
@BatchSize을 추가한다. -
이 옵션을 사용하면 컬렉션이나, 프록시 객체를 한꺼번에 설정한 size 만큼 IN 쿼리로 조회한다.
-
OrderRepository에 추가
@Repository @RequiredArgsConstructor public class OrderRepository { private final EntityManager em; // 재사용성 O public List<Order> findAllWithMemberDelivery() { return em.createQuery( "select o from Order o" + " join fetch o.member m" + " join fetch o.delivery d", Order.class ).getResultList(); } }OrderApiController에 추가
/** * V3.1 엔티티를 조회해서 DTO로 변환 페이징 고려 *-ToOne 관계만 우선 모두 페치 조인으로 최적화 * - 컬렉션 관계는 hibernate.default_batch_fetch_size, @BatchSize로 최적화 */ @RestController @RequiredArgsConstructor public class OrderApiController { private final OrderRepository orderRepository; @GetMapping("/api/v3.1/orders") public List<OrderDto> ordersV3_page(@RequestParam(value = "offset", defaultValue = "0") int offset, @RequestParam(value = "limit", defaultValue = "100") int limit) { List<Order> orders = orderRepository.findAllWithMemberDelivery(offset, limit); List<OrderDto> result = orders.stream() .map(o -> new OrderDto(o)) .collect(toList()); return result; } }최적화 옵션 - 글로벌
spring: jpa: properties: hibernate: default_batch_fetch_size: 1000-
만약, 글로벌 설정이 아닌 개별로 설정하려면
@BatchSize를 적용하면 된다. -
이렇게 최적화 옵션을 적용하면 다음과 같은 장점이 존재한다.
-
쿼리 호출 수가
1 + N->1 + 1로 최적화 된다. (N+1 문제 해결) -
조인보다 DB 데이터 전송량이 최적화 된다. (Order와 OrderItem을 조인하면 Order가 OrderItem 만큼 중복해서 조회된다. 이 방법은 각각 조회하므로 전송해야할 중복 데이터가 없다)
-
페치 조인 방식과 비교해서 쿼리 호출 수가 약간 증가하지만, DB 데이터 전송량이 감소한다.
-
컬렉션 페치 조인은 페이징이 불가능하지만, 이 방법은 페이징이 가능하다.
-
-
결론
-
ToOne관계는 페치 조인해도 페이징에 영향을 주지 않는다. -
따라서
ToOne관계는 페치 조인으로 쿼리 수를 줄이고, 나머지는hibernate.default_batch_fetch_size로 최적화하자.
-
-
참고로,
default_batch_fetch_size의 크기는 100 ~ 1000 사이 선택하는 것을 권장한다. DB에 따라 IN 절 파라미터를 1000으로 제한하기도 한다.-
예시) 1000으로 잡으면 한번에 1000개를 DB에서 애플리케이션에 불러오므로 DB에 순간 부하가 증가할 수 있다.
-
하지만 애플리케이션은 100이든 1000이든 결국 전체 데이터를 로딩해야 하므로 메모리 사용량이 같다.
-
즉, DB든 애플리케이션이든 순간 부하를 어디까지 견딜 수 있는지로 결정하면 된다.
-
Review
컬렉션이 포함된 조회인 경우 어떻게 해야 최적화 되는지 알게 되는 강의였다.
다대일, 일대일 관계처럼
ToOne관계는 페치 조인으로 하고 일대다 관계인ToMany인 경우 개별적으로@BatchSize하거나 또는 글로벌 설정으로hibernate.default_batch_fetch_size을 적용하자.이번 시간에는
엔티티 조회를 기준으로 컬렉션에 대한 조회를 최적화하는 방법을 정리했다.다음 시간에는
DTO 직접 조회를 기준으로 컬렉션에 대한 조회를 최적화 하는 방법을 정리해보자.Reference
-
- DevHistory 4
- Essay 1
- Java 10
- Spring 15
- SpringBoot 17
- JPA 13
- MySQL 3
- Flyway 1
- Kafka 8
- Technology 22
- GoodCode 7
- Side_Project 20
- Retrospective 4
- AlgorithmSkill 3
- LeetCode 2
- Algorithm 70
- SQL 9
- OS 14
- Database 8
- Network 7
- HTTP 7
- DataStructure 5
- Linux 4
- Woowacourse 4
- Git 9
- AssertJ 1
- IntelliJ 5
- Probability-Statistics 5
- Electronic-Finance 13
- Business-Statistics 13
- Competition 1
- Book 6
- Workout 7
- E.T.C 8