지금의 기록이 미래의 자산이 된다.
Today's records become tomorrow's assets.-
[우아한테크코스] 코수타 내용 정리

-
우아한테크코스에서 왼손님과 포비님이 유튜브로 진행한 코수타에서
-
제 기준으로 중요한 내용 혹은 알면 좋은 내용들을 정리해봤습니다.
-
자세한 얘기를 듣고 싶은 분들은 아래의 링크(URL)를 통해 들어주시면 좋을 것 같습니다!
우아한테크코스 코수타 URL
우아한테크코스 5기 OT
스스로 문제를 해결하자.- 우테코 취지
-
취업 준비생을 위한 10개월간 무료교육과정
-
현장지향형 교육 운영
-
독학으로 3~6개월간 독학한 친구들이 프리코스를 참여한다면, 합격할 수 있다고 본다.
-
- 우테코 지향, 주요부분
-
함께 하는 교육자분들이 현장 경험이 최소 2년 이상인 게 장점이라 본다.
-
level 1,2는 과제 진행 → 현장 개발자들에게 1대1 코드 리뷰를 받아볼 수 있다.
-
강의식, 이론 기반보다는 실무+능동+주도적인 교육기관이다.
-
- 프리코스
-
과제 기반 교육을 운영
-
강의는 최소한으로 할 예정
-
*짧은 기간 동안 코드에 대해서 읽기 좋은, 유지 보수, 리팩토링 → 경험들을 배울 것임.
-
- 프리코스 커뮤니티
-
함께 성장, 학습하기 위해서 만든 커뮤니티. - 크게 3가지 활동
-
peer 코드 리뷰 - 서로 의견 공유
-
아고라 - 학습에 관련한 토론, 질의응답
-
학습 컨텐츠 공유 - 내가 학습을 해서 블로그나 외부 학습자료를 공유
-
스스로 먼저 해보는게 중요하다. (자기주도학습)
-
2주차 첫번째 부터 시작한다.(11월 1일)
-
- 과제 피드백
-
1주차 끝난 이후에, 코치분들이 공통 피드백을 나갈거다.
-
다음 주차에 공통 피드백을 반영할 예정이다.
-
-
-
-
1-2. Introduction to OS
이 글의 사진과 내용은 공룡책 과 컴퓨터학부 수업인 운영체제 강의자료를 기반으로 작성했습니다.
1. 운영체제의 정의
OS는 컴퓨터 하드웨어 바로 윗단에 설치되는 소프트웨어.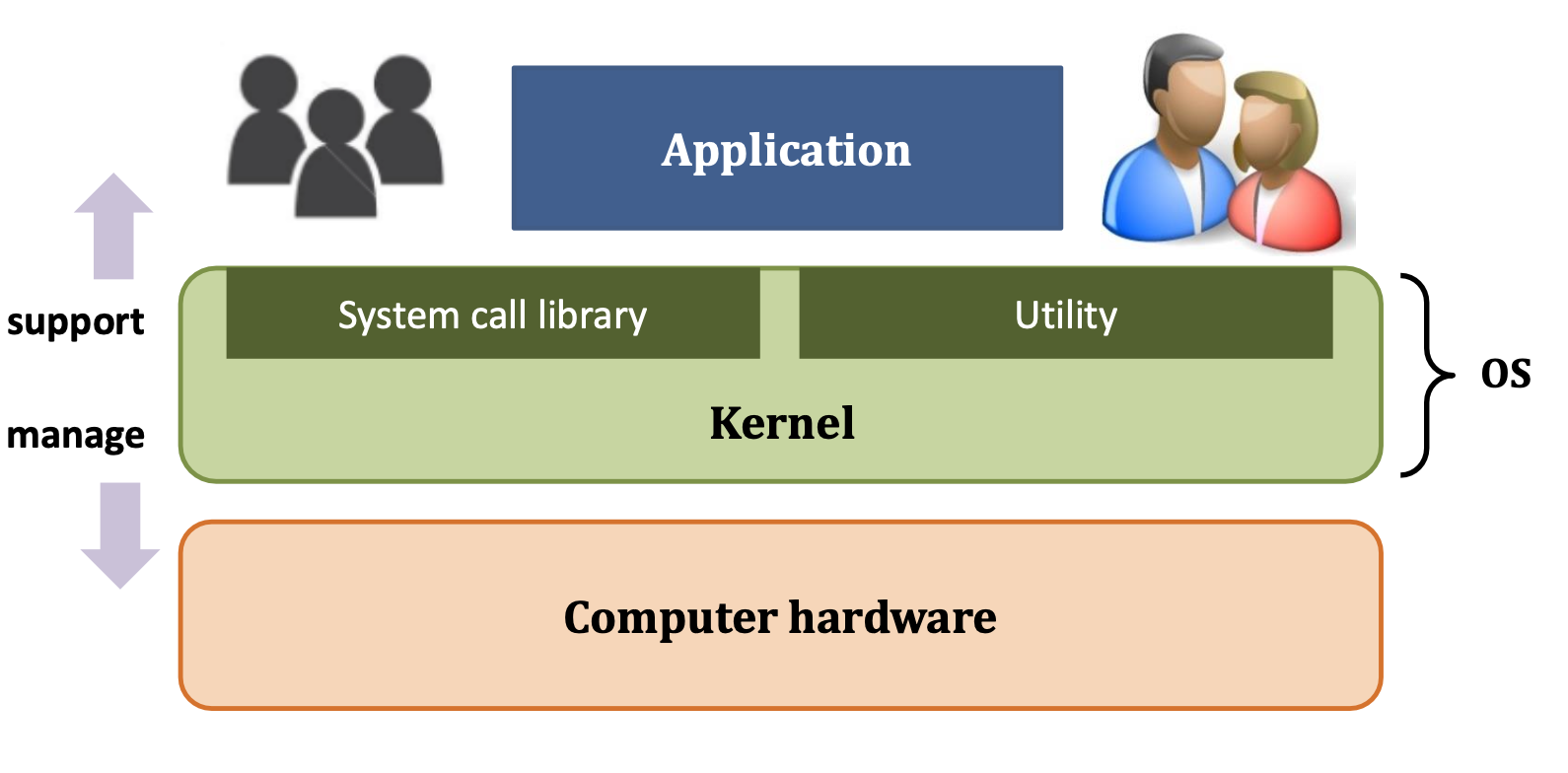
-
각종 SW들은 위의 그림과 같이 HW와 OS가 한 몸으로 존재하는 컴퓨터 시스템 위에서 수행되는 것으로 볼 수 있다.
-
컴퓨터 전원을 On 하면, OS는 이와 동시에 실행된다.
-
OS 중 항상 필요한 부분만을 전원이 On과 동시에 메모리에 올려놓고 그렇지 않은 부분은 필요할 때 메모리에 올려서 사용하게 된다.
-
이때 메모리에 상주하는 운영체제의 부분을
커널(kernel)이라고 부르며 이를 좁은 의미의 운영체제라고도 부른다. -
즉 커널은 운영체제 코드 중에서도 핵심적인 부분을 뜻한다.
2. 운영체제의 기능

컴퓨터 HW와 User 사이에 OS가 존재하므로, OS의 역할은
HW를 위한 역할과User를 위한 역할의 두 가지로 나누어볼 수 있다.-
HW쪽에서는 User가 직접 다루기 힘든 각종 HW를 OS가 관리하는 역할을 하며,User에게는 편리한 Interface를 제공하는 역할을 한다. -
OS의 두 가지 주요 기능
-
[1] 컴퓨터 시스템 내의 자원을 효율적으로 관리하는 것 -> 중요한 핵심 기능
-
[2] .컴퓨터 시스템을 편리하게 사용할 수 있는 환경을 제공하는 것
-
-
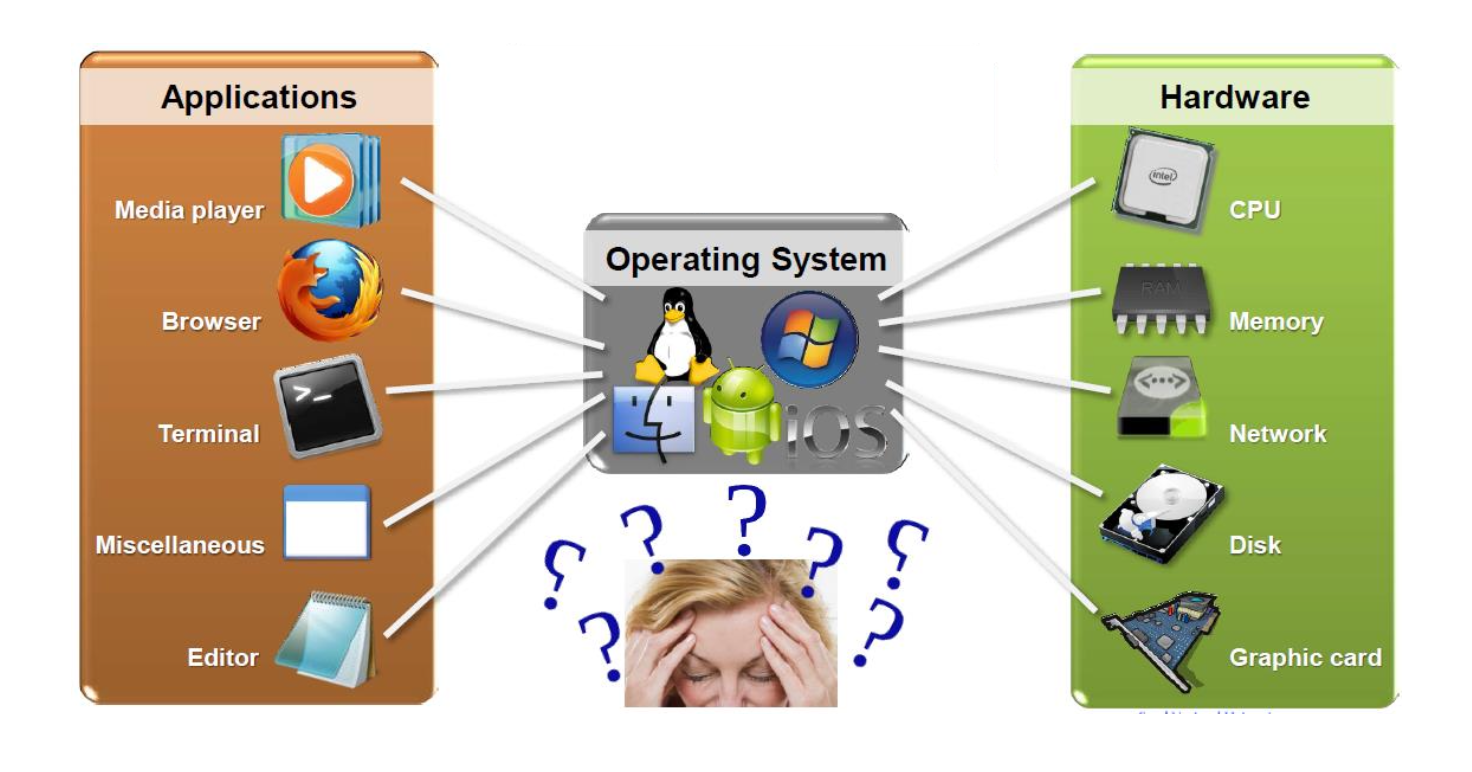
OS를
자원관리자(resource manager)라고 부르기도 한다.- 여기서
자원이란 CPU, Memory, HardDisk 등 HW 자원뿐 아니라 SW 자원까지를 통칭해서 부르는 말이다.
- 여기서
-
OS는 사용자 및 프로그램들 간에 자원이 형평성 있게 분배되도록 하는
균형자역할도 함께 수행해야 한다. -
효율성이 가장 큰 목표이지만 이로 인해 일부가 지나치게 희생되지 않게 하는 형평성 역시 OS가 고려해야할 목표이다.
-
이 밖에도 OS는 사용자와 OS 자신을 보호하는 역할을 담당하기도 한다.
3.운영체제의 분류
OS를 분류하는 기준
동시 작업이 있다.-
동시 작업을 지원하는 여부
-
단일작업용 OS : 한 번에 하나의 프로그램만 실행 시킬 수 있다.
-
다중작업용 OS : 2개 이상의 프로그램을 처리할 수 있다.
-
-
OS가 다중작업을 처리할 때에는 여러 프로그램이 CPU와 메모리를 공유하게 된다. 참고로 컴퓨터 1개당 CPU는 1개만 존재한다.
-
하지만, CPU의 처리 속도가 워낙 빨라 짧은 시간의 규모로 여러 프로그램들이 CPU에서 번갈아 실행된다. 그렇기 때문에 사용자 입장에서는 여러 프로그램이 동시에 실행되는 것처럼 보인다. 이와 같이 CPU의 작업시간을 여러 프로그램들이 조금씩 나누어 쓰는 시스템을
시분할 시스템이라고 부른다. -
CPU와 달리
메모리의 경우 여러 프로그램들이 조금씩 메모리 공간을 보유하며 동시에 메모리에 올라가 있을 수 있다. 이처럼 메모리 공간을 분할해 여러 프로그램들이 동시에 메모리에 올려놓고 처리하는 시스템을다중 프로그래밍 시스템이라고 부른다. -
다중작업용 OS경우 여러 프로그램을 같이 실행시키지만
- 사용자 입장에서는 각 프로그램에 대한 키보드 입력의 결과를 화면에 보여주기 때문에 이러한 시스템을
대화형 시스템이라고 부른다.
- 사용자 입장에서는 각 프로그램에 대한 키보드 입력의 결과를 화면에 보여주기 때문에 이러한 시스템을
-
다중작업, 시분할, 다중 프로그래밍, 대화형 시스템은 모두 여러 프로그램이 하나의 컴퓨터에서 동시에 실행된다.
-
다중처리기 시스템은 하나의 컴퓨터 안에 CPU가 여러 개 설치된 경우를 뜻하므로 앞의 용어들과는 의미가 다르다. -
CPU가 여럿 있는 컴퓨터는 서로 다른 CPU에서 여러 프로그램이 동시에 실행될 수 있어 처리가 더욱 빨라지지만,
- OS입장에서는 여러 CPU를 관리하기 위해 더욱 복잡한 메커니즘을 필요로 한다.
OS를 분류하는 또다른 기준은
다중 사용자에 대한 동시 지원이다.- 단일 사용자용 OS : 한 번에 한 명의 사용자만이 사용하도록 허용하는 OS (ex. DOS)
- 다중 사용자용 OS : 여러 사용자가 동시에 접속해 사용할 수 있게 하는 OS (ex. 이메일 서버, 웹 서버)
OS를 분류하는 또 다른 기준은
작업을 처리하는 방식이다.
-
-
Spring MVC 패턴
Spring MVC
MVC란 ?
- 소프트웨어 설계와 관련된 디자인 패턴으로, 소프트웨어 공학에서의 ‘흔히 사용되는’ 설계 패턴을 의미한다.
MVC 가 생겨난 이유
-
코드가 많아지고 길어질수록 나중에 기능을 수정할때마다 코드를 갈아엎어야 하는 경우가 많다.
-
한마디로 유지보수가 너무 불편한 경우가 있다.
-
그래서 프로그래머들이 유지보수성, 애플리케이션의 확장성, 그리고 유연성이 증가하고, 중복코딩이라는 문제점 또한 사라지는 효과를 가질 수 있기 때문에 Spring MVC라는 구조를 만들었다.
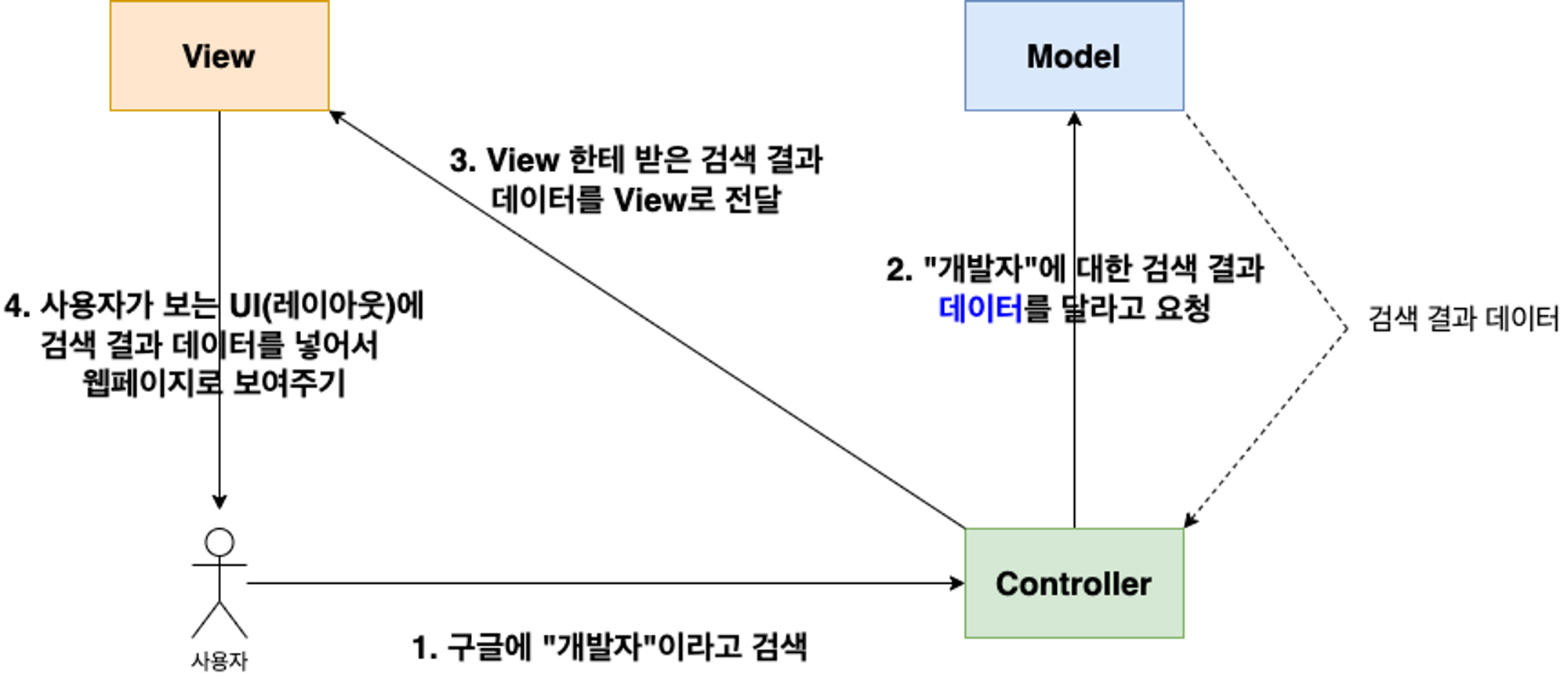
MVC 구조 맛보기
-
Model : 데이터와 관련된 부분
-
View : 사용자한테 보여지는 부분
-
Controller : Model과 View를 이어주는 부분
MVC를 지키면서 코딩하는 방법
-
Model은 Controller와 View에 의존하지 않아야 한다.(Model 내부에 Controller와 View에 관한 코드가 있으면 안된다.)
-
View는
Model에만 의존해야하고, Controller에는 의존하면 안된다. (View 내부에 Model 코드만 있을 수 있고, Controller 코드는 있으면 안된다.) -
View가 Model로부터 데이터를 받을 때, 사용자마다 다르게 보여주어야 하는 데이터에 대해서만 받아야 한다.
-
Controller는
Model과View에 의존해도 된다.(Controller 내부에는 Model과 View의 코드가 있을 수 있다.) -
View가 Model로부터 데이터를 받을 때, 반드시 Controller에서 받아야 한다.
-
IntelliJ 유용한 단축키들 (Mac 기준)
-
Mac기준으로 인텔리제이를 쓰면서 유용한 단축키 기능들을 정리해보려고 한다.
-
정리한 이후에도 유용한 단축키를 알게되면 추가적으로 업로드를 할 예정이다.
단축키
Getter & Setter 추가 / this 추가 / toString 추가
-
cmd + n을 눌러서 Getter & Setter을 클릭하고 원하는 변수를 선택하여 ok 버튼을 클릭하면 자동으로 추가된다. -
cmd + n을 눌러서 Constructor을 클릭하여 위와 같은 방식으로 처리하면 this가 자동으로 추가된다. -
cmd + n을 눌러서toString을 입력하여 클릭하고 위와 같은 방식으로 처리하면 toString이 자동으로 추가된다.
Import 추가 / 이름 변경(클래스, 메서드 , 패키지)
-
import가 필요한 경우
option + enter를 누르면 “Implement methods” 를 선택한 다음에 -
해당 변수들을 선택하고 ok버튼을 클릭하면 다음과 같이 자동으로 추가된 것을 확인할 수 있다.
-
이름을 변경하고 싶으면
option + enter를 누르고 “Rename file”을 선택하면 된다.
변수 (세미콜론까지) 자동으로 입력
cmd + shift + enter누르면 세미콜론까지 자동으로 입력된다.
자동 정렬 기능
cmd + option + L을 누르면 자동으로 정렬이 된다.
변수 선언 및 return 부분을 합치는 기능
방법1 :
control + t누르고 Inline Variable 클릭하면 된다.방법2 :
cmd + option + n(Inline Variable 단축키)방법2 예시
[변경 전]
public class MemberRepository { /* ... */ public List<Member> findALl() { List<Member> result = em.createQuery("select m from Member m", Member.class) .getResultList(); return result; } }- 변수를 선언한 이후에 해당 {} 안을 깔끔하게 합치려면,
cmd + option + n을 누르면 다음과 같이 단축된다.
[변경 후]
public class MemberRepository { /* ... */ public List<Member> findALl() { return em.createQuery("select m from Member m", Member.class) .getResultList(); } }
-
-
자바의 기본 개념 1편
Java
-
자바 언어는 플랫폼에 독립적으로 설계되었다.
-
자바 코드는 운영체제나 CPU 등 플랫폼에 상관없이 자바 가상 기계(JVM)만 있으면 어떤 컴퓨터에서든 동일하게 실행된다. 이를 WORA(Write Once Run Anywhere) 라고 한다.
-
한 번 작성된 자바 프로그램은 수정 없이 실행 가능하다.
자바 가상 기계와 바이트 코드
-
바이트 코드(byte code)는 자바 컴파일러가 자바 소스 프로그램을 컴파일한 일종의 기계어로서, 자바 가상 기계(Java Virtual Machine, JVM)에 의해 실행되는 바이너리 코드(binary code)이다.
-
바이트 코드는 자바 가상 기계에 의해 인터프리터 방식으로 한 명령씩 해석되어 실행된다.
-
자바 프로그램 입장에서 볼때 자바 가상 기계는 운영체제이자 컴퓨터이다.
-
자바 가상 기계는 플랫폼에 적합하게 서로 다르게 구현되므로 플랫폼 종속적이다.
자바 응용프로그램 실행 환경
-
자바 컴파일러는 자바 소스 프로그램을 컴파일하여 바이트 코드를 클래스 파일(class file)에 저장한다.
-
자바 프로그램이 실행되기 위해서는 개발자가 작성한 자바 프로그램 외에 자바 플랫폼에서 제공하는 다양한 클래스 라이브러리(자바 APIs)가 반드시 필요하다.
자바와 타언어(C/C++)의 실행 차이
-
C/C++는 컴파일한 목적 파일을 링크시켜 하나의 실행파일(exe)을 만들며, 이 실행 파일 하나만 있으면 실행 가능하다. 그리고 이 실행 파일은 컴퓨터의 CPU가 바로 실행한다.
-
Java의 경우 링크 과정이 없으며 자바 가상 기계가 컴파일된 클래스 파일을 실행한다.
JDK와 JRE
-
JDK(Java Development Kit)는 자바 개발자를 위한 상업용 소프트웨어로, 자바 컴파일러 등의 개발 도구와 JRE(Java Runtime Environment)로 구성된다.
-
JRE는 자바 응용프로그램이 실행될 때 필요한 소프트웨어들로 개발자가 활용할 수 있는 자바 API(이미 컴파일된 다양한 클래스 라이브러리)와 자바 가상 기계를 포함한다.
자바 API
- 자바 API(Application Programming Interface)는 개발자들이 사용하도록 미리 만들어놓은 유용한 자바 클래스들의 집합이다.
이클립스, 자바 통합 개발 환경
-
IDE(Integrated Development Environment)란 소스 코드 편집, 컴파일, 디버깅을 한꺼번에 할 수 있는 소프트웨어 통합 개발 환경을 일컫는다.
-
C/C++ → 비주얼 스튜디오 / Java → 이클립스(eclipse)
-
이클립스는 자바 언어로 개발된 데스크톱 응용프로그램이다.
자바의 특징
-
플랫폼 독립성 - 자바 가상 기계만 있으면 자바 프로그램의 실행이 가능하다.
-
객체 지향 - 캡슐화, 상속, 다형성 등을 지원한다. 객체 지향 프로그램은 해결할 과제를 실제 세상의 객체와 객체간의 상호 관계로 모델링하여 인간의 사고에 가깝게 표현한다.
-
클래스로 캡슐화 - 자바는 변수나 메소드는 반드시 클래스 내에 구현하도록 한다.
-
소스와 클래스 파일 - 자바 소스가 컴파일된 클래스 파일(.class)는 반드시 하나의 자바 클래스만이 들어있다.
-
실행 코드 배포 - 다수의 클래스 파일을 jar 파일 형태로 압축하여 배포 및 실행이 가능하다.
-
패키지 - 서로 관련 있는 클래스는 패키지로 묶어 관리한다.
-
멀티스레드 - 하나의 자바 프로그램에서 다수의 스레드가 동시에 실행할 수 있는 환경을 지원한다.
-
가비지 컬렉션 - 자바 언어는 메모리를 반환하는 기능이 없다. 프로그램 내에 사용되지 않는 메모리는 자바 가상 기계의 가비지 컬렌셕 기능에 의해 자동으로 회수된다.
-
실시간 응용 시스템에 부적합 - 자바 응용프로그램은 실행 도중 예측할 수 없는 시점에 가비지 컬렉션이 실행되므로, 프로그램이 일시적으로 중단된다.
Reference
- 책 - 명품 자바 에센셜
-
- DevHistory 4
- Essay 1
- Java 10
- Spring 15
- SpringBoot 17
- JPA 13
- MySQL 3
- Flyway 1
- Kafka 8
- Technology 22
- GoodCode 7
- Side_Project 20
- Retrospective 4
- AlgorithmSkill 3
- LeetCode 2
- Algorithm 70
- SQL 9
- OS 14
- Database 8
- Network 7
- HTTP 7
- DataStructure 5
- Linux 4
- Woowacourse 4
- Git 9
- AssertJ 1
- IntelliJ 5
- Probability-Statistics 5
- Electronic-Finance 13
- Business-Statistics 13
- Competition 1
- Book 6
- Workout 7
- E.T.C 8