지금의 기록이 미래의 자산이 된다.
Today's records become tomorrow's assets.-
2024 Dev History
2024 Dev History
- 2023 Dev History에 이어 2024년에도 내가 공부하면서 배운 내용을 꾸준히 기록해두자.
Plan
인프런 강의: 우아한형제들 최연소 기술이사 김영한의 스프링 완전 정복
인프런 강의: 김영한의 스프링 부트와 JPA 실무 완전 정복 로드맵
인프런 강의: Kotlin
서버 개발과 관련된 책
개인 프로젝트: Hibit (version 2)
- [Hibit] (ver.2) - Github : 기존 version1 에 개발했던 백엔드 코드와 구조를 개선하기 위해 version2로 디벨롭시킨 프로젝트
A Weekly Record
January to June
240101 ~ 240107
-
[Programmers] SQL - Join 문제 - 오랜 기간 보호한 동물(1), 없어진 기록 찾기(1), 있었는데요 없었습니다, 주문량이 많은 아이스크림 조회하기
240108 ~ 240114
-
[Spring MVC 2편] 파일 업로드, 다운로드 강의 수강
240115 ~ 24021
240122 ~ 240128
240129 ~ 240204
240205 ~ 240211
240226 ~ 240303
240311 ~ 240317
-
[Kotlin] 자바 개발자를 위한 코틀린 입문 강의 - 정리
-
섹션1. 코틀린에서의 변수와 타입, 연산자를 다루는 방법
-
섹션2. 코틀린에서 코드를 제어하는 방법
-
섹션3. 코틀린에서의 OOP
-
섹션4. 코틀린에서의 FP
-
240318 ~ 240324
-
[Kotlin] 실전! 코틀린과 스프링 부트 실습 강의 - 정리
-
섹션1. 도서관리 애플리케이션 리팩토링 준비하기
-
섹션2. Java 서버를 Kotlin 서버로 리팩터링하자!
-
섹션3. 첫 번째 요구사항 추가하기 - 책 분야 (Enum 활용)
-
섹션4. 두 번째 요구사항 추가하기 - 도서 대출 현황 (N+1 문제 해결)
-
240325 ~ 240331
240429 ~ 240505
240621
July to December
240819 ~ 240825
240902 ~ 240908
240909 ~ 240915
240916 ~ 240922
2401021 ~ 241027
241028 ~ 241103
20241104 ~ 20241110
20241118 ~ 20241124
20241209 ~ 20241215
20241231
-
2023년 회고
2023년은 20대 동안
개발면에서 가장 활발하게 다양한 활동을 경험한 한 해이자, 휴식이 적은 한 해였다. 정말 순식간에 1년이 지나가버린 것 같다 🤔.그동안 내가 무엇을 배웠고 어떤 성장을 했는지 하나씩 정리해보자. ✍🏻
2023년에 내가 공부하면서 배운 내용을 2023 Dev History에도 기록해두었다.
2023년에 참여한 모임 1월 ~ 5월: 신입 개발자를 위한 CS 스터디 모임 3월 ~ 11월: 히빗(팀 프로젝트) (8월: 대학교 졸업) 4월 ~ 9월: 우리FISA '클라우드 서비스 개발자' 8월 ~ 9월, 12월: 굿프렌즈(팀 프로젝트) 11월 ~ 12월: 우아한스터디 2023 겨울시즌 '내 코드가 그렇게 이상한가요?' 12월: 글또 9기 '글 쓰는 또라이가 세상을 바꾼다! 글쓰는 개발자 모임'신입 개발자를 위한 CS 스터디 모임
2023년 1월에 시작한 신입 개발자를 위한 CS 스터디 5월 말까지 5개월 동안 지속적으로 운영해왔다. 그 당시에는 컴퓨터 기반 지식이 부족했고, 배워야 할 것이 너무 많아서 운영체제, 데이터베이스, 네트워크와 같은 컴퓨터 공학의 필수 과목을 매월 1개씩 스터디원들과 공부해나갔다.
스터디를 처음 운영해보는 경험이라 깊이 있는 학습과 철저한 기록을 목표로 삼았다. 그래서 우리 스터디의
목표는 CS 기본 지식들을 깊이 있게 습득하고, 공부한 내용을 설명하여 죽은 지식이 아닌 살아있는 지식으로 바꾸고자 했다. 여러 시행착오를 거치면서 더 나은 개선 방향을 찾고, 이러한 경험을 Issues와 Wiki에 정리해놓았다.-
Issues에는 주제와 내용을 매주 정하고, 각 스터디원이 주제를 정해 발표하는 내용을 기록했다.
-
Wiki에는 외부인도 쉽게 이해할 수 있도록 주제를 카테고리별로 정리하고, 주차별로 기록했다.
5개월 동안 진행한 뒤 6월부터는 다른 교육과 사이드 프로젝트로 인해 참석하지 못했지만, 남아있는 스터디원들이 적극적으로 활동하여 12월 31일 현재까지 총 591개의 Star를 받게 되었다. 이는 1-3월에 80개, 5월에 150개, 11월에 500개로 거의 매일 Star가 증가한 것을 보며 뿌듯함과 신기함을 느끼게 되었다.
이 스터디가 많은 Star를 받은 이유는 다른 CS 스터디 모임보다 CS 지식을 깊게 공부하고 정리한 점과 외부 사람이 이해하기 쉽도록 작성하려고 노력한 점이라고 생각한다. 현재까지도 스터디원분들끼리 매주 온라인 회의로 스터디를 진행하시는데, 이런 분들과 같이 스터디를 할 수 있어서 영광이라고 생각한다 👏🏻.
해당 스터디에서 배운 내용은 아래와 같다.
신입 개발자를 위한 CS 스터디 모임에서 진행했던 내용
- 데이터베이스 - 학교에서 배운 전공 서적, 데이터베이스 개론, 면접을 위한 CS 전공지식 노트 + 그 외에 각종 레퍼런스 자료들
- 운영체제 - 학교에서 배운 전공 서적, Operating Systems: Three Easy Pieces , 운영체제와 정보기술의 원리, 면접을 위한 CS 전공지식 노트 + 그 외에 각종 레퍼런스 자료들
- 네트워크 - 학교에서 배운 전공 서적, 면접을 위한 CS 전공지식 노트 + 그 외에 각종 레퍼런스 자료들
- 자료구조 - 학교에서 배운 전공 서적, 면접을 위한 CS 전공지식 노트 + 그 외에 각종 레퍼런스 자료들
Spring, JPA 부분은 김영한의 스프링 완전 정복에 있는 강의를 혼자서 들으면서, 관련 내용을 블로그에 정리했다.
-
-
[Programmers] 118667. 두 큐 합 같게 만들기(queue)
성능 요약
-
메모리: 119 MB, 시간: 49.53 ms - Answer Code1
-
메모리: 98.7 MB, 시간: 4.72 ms - Answer Code2
구분
- 코딩테스트 연습 > 2022 KAKAO TECH INTERNSHIP
Answer Code1(2023.12.28)
import java.util.*; class Solution { public int solution(int[] queue1, int[] queue2) { Queue<Integer> que1 = new LinkedList<>(); Queue<Integer> que2 = new LinkedList<>(); long sum1 = 0, sum2 = 0; for(int i = 0; i < queue1.length; i++) { sum1 += queue1[i]; que1.offer(queue1[i]); } for(int i = 0; i < queue2.length; i++) { sum2 += queue2[i]; que2.offer(queue2[i]); } int count = 0; while(sum1 != sum2) { count++; if(sum1 > sum2) { int value = que1.poll(); sum1 -= value; sum2 += value; que2.offer(value); } else { int value = que2.poll(); sum1 += value; sum2 -= value; que1.offer(value); } if(count > (queue1.length + queue2.length) * 2) return -1; } return count; } }문제풀이
-
각 큐의 합이 같을 때까지 반복문을 돌려줬다.
-
또한 원소의 합이 같지 않는 경우에는 return을 -1로 두는 특수 예외 조건이 존재한다.
-
분기 조건이
(queue1.length + queue2.length) * 2인 이유는 양쪽 큐 길이를 전부 돌았을 횟수로 잡았기 때문이다. -
즉, 각 큐에서 원소를 추출하고 집어넣는 작업이 최대로 반복될 수 있는 횟수를 고려한 것이다.
-
최악의 경우, 한 큐의 모든 원소를 다른 큐에 집어넣어야 할 수 있으므로, 이때 루프의 최대 횟수는 큐의 길이의 2배가 된다.
-
-
합계(sum)가 long 형으로 한 이유는
제한사항에서 queue1, queue2 원소의 최대 범위가 10^9이므로, 합 계산 과정 중 산술 오버플로우 발생 가능성이 있어서이다.
Answer Code2(2023.12.28)
import java.util.*; class Solution { public int solution(int[] queue1, int[] queue2) { int[] totalQueue = new int[queue1.length + queue2.length]; long queue1Sum = 0; long queue2Sum = 0; for(int i = 0; i < queue1.length; i++) { int val = queue1[i]; totalQueue[i] = val; queue1Sum += val; } for(int i = queue1.length; i < queue1.length + queue2.length; i++) { int val = queue2[i - queue1.length]; totalQueue[i] = val; queue2Sum += val; } if((queue1Sum + queue2Sum) % 2 == 1) return -1; int count = 0; int left = 0; int right = queue1.length; long half = (queue1Sum + queue2Sum) / 2; while(left < right && right < totalQueue.length) { if(queue1Sum == half) { return count; } else if(queue1Sum > half) { queue1Sum -= totalQueue[left++]; } else { queue1Sum += totalQueue[right++]; } count++; } return -1; } }
-
-
Git 형상 관리 + 작업 단위와 PR 코드 리뷰 + 협업을 잘하는 개발자 (feat. 제미니의 개발실무)
이 글은 제미니의 개발실무의 Git 형상 관리 + 작업 단위와 PR 코드 리뷰 + 협업을 잘하는 개발자 영상을 보면서 제 생각과 같이 정리한 글입니다.
(시청자) 질문. 큰 규모의 작업을 할 때 commit 해야 할 작업 task를 나누는 기준이 궁금합니다.
- commit 할 작업 단위를 먼저 생각해보고 -> 그 단위로 작업을 하면서 중간중간 commit한다.
- 그냥 한번에 기능 단위 개발을 하고 -> 이후에 작업을 쪼개면서 commit한다.
작업 task를 나누는 기준
-
리뷰시스템 전체를 개발한다고 가정을 해보자. 그러면 하나의 task로 담기에는 굉장히 클 수 있다. -
그렇기 때문에 먼저
작업 단위 자체를 잘 나누는게 가장 중요하다. -
리뷰라는 기능이 있다면,리뷰 등록, 리뷰 삭제와 같은 각 세부 기능에 대해서
하나의 작업이라 생각하고, 그러한 작업을Issue & Branch & PR로 가져가는게 좋다.큰 규모의 작업 자체가 있으면, 이는 여러가지 어려움을 만드는 것 같다.
추가/수정된 파일과 커밋 갯수가 많을 수록 다른 사람이 코드 리뷰하는게 까다로울 수 있다.
-
제민님의 의견: 같이 일하는 동료가 내 코드를 쉽게 이해할 수 있도록 task를 작게 가져갈 것 같다.
작업 단위를 작게 나누고, 위에 질문주신 2가지를 고민할 것 같다.
작업 단위를 작게 엄청 잘 나누게 되면, 애초에 커밋에 대한 생각을 많이 안해도 되는 경우가 있는 것 같다.
흔히 많이 하는 실수가 신규 기능 개발과 리팩터링하는 것을
하나의 task라고 생각하고 작업하는 경우가 있다.이러한 실수를 예방하기 위해 한 가지 작업을 딱 정해서, 최대한 작게 가져가면 커밋에 대한 고민은 크게 하지 않아도 된다.
즉, 신규 기능 개발과 리팩터링을 각각의 작업 단위로 생각해야 한다. -> task1 : 신규 기능 개발 / task2 : 리팩터링
-
결론적으로 질문 주신 것에 대해 답변을 하면, 1번과 2번을 다 쓰긴 한다.
어떻게 하면 동료가 코드 리뷰하기 더 좋을까에 대해서 커밋과 PR를 나눈다고 보시면 될 것 같다.
커밋하는 부분도 협업 스킬 중 하나
-
개인적으로 2번을 많이 쓴다. 2번: “그냥 한번에 기능 단위 개발을 하고 -> 이후에 작업을 쪼개면서 commit한다.”
커밋하는 부분도 협업 스킬 중 하나라고 생각한다.
-
아래와 같이 커밋을 작성하면 리뷰하는 사람 입장에서 힘들 수 있다.
User 클래스에 대한 작업 <- 하나의 task --- 아래부터는 커밋 내용 feat: User 클래스가 수정! feat: User 클래스가 수정! feat: User 클래스가 수정! (리팩토링 포함) feat: User 클래스가 수정! ... feat: User 클래스가 수정! [PR] 수정 파일이 50개 커밋이 10개-
만약 작업 단위가 작았다면, 위에서처럼 발생할 수 없다.
수정 파일이 많고, 같은 클래스에서 여러 번의 커밋을 작성하면, 리뷰할 사람 입장에서는 이해하기가 어려울 수 있다.
-
[PR 올릴 때 커밋 정리 기준 중 하나] - 한 클래스는 한 파일에서만 수정된다.
-
보통 커밋은 아래와 같이 진행한다.
-
하나의 작업에 대한 커밋을 여러번 작성한다. -> 본인을 위해
-
어느 정도 커밋을 작성하고 PR을 올리기 전에, 지금까지 작성한 커밋들을 정리한다.
-
PR을 올리면서 동료로부터 코드 리뷰를 받고, 추가적인 커밋을 한다. -> 동료를 위해
-
리뷰가 끝나면, 지금까지 작성한 커밋을 한번 더 정리를 한다. -> 회사 자산 관리 + 미래의 동료를 위해
- 이런 관점으로 접근해서 형상 관리를 하고 있다.
브랜치 작성 방법
-
리뷰에 대한 기능을 개발한다고 가정했을 때, 작업 단위를 나눈다. -> 리뷰 등록, 리뷰 조회, 리뷰 수정, 리뷰 삭제 -
그런 다음, 작업에 대한 Branch를 나누고 PR도 여러개 올린다.
-
리뷰 등록에 대한 Branch명:
review-add -
리뷰 삭제에 대한 Branch명:
review-remove
-
-
그리고 세부 기능에 대해서 Branch를 연계적으로 생성한다.

Review
-
이전 굿프렌즈 팀 프로젝트에서는 우리만의 Git flow 전략을 만들면서, 형상 관리를 나름 신경썼다고 생각했다.
-
브랜치 면에서는 이 영상에서 다루는 거와 거의 비슷하게 작업을 진행했지만, 커밋 부분에 있어서는 ‘이 정도로 신경을 써야 하는구나’라는 생각이 많이 들었다.
-
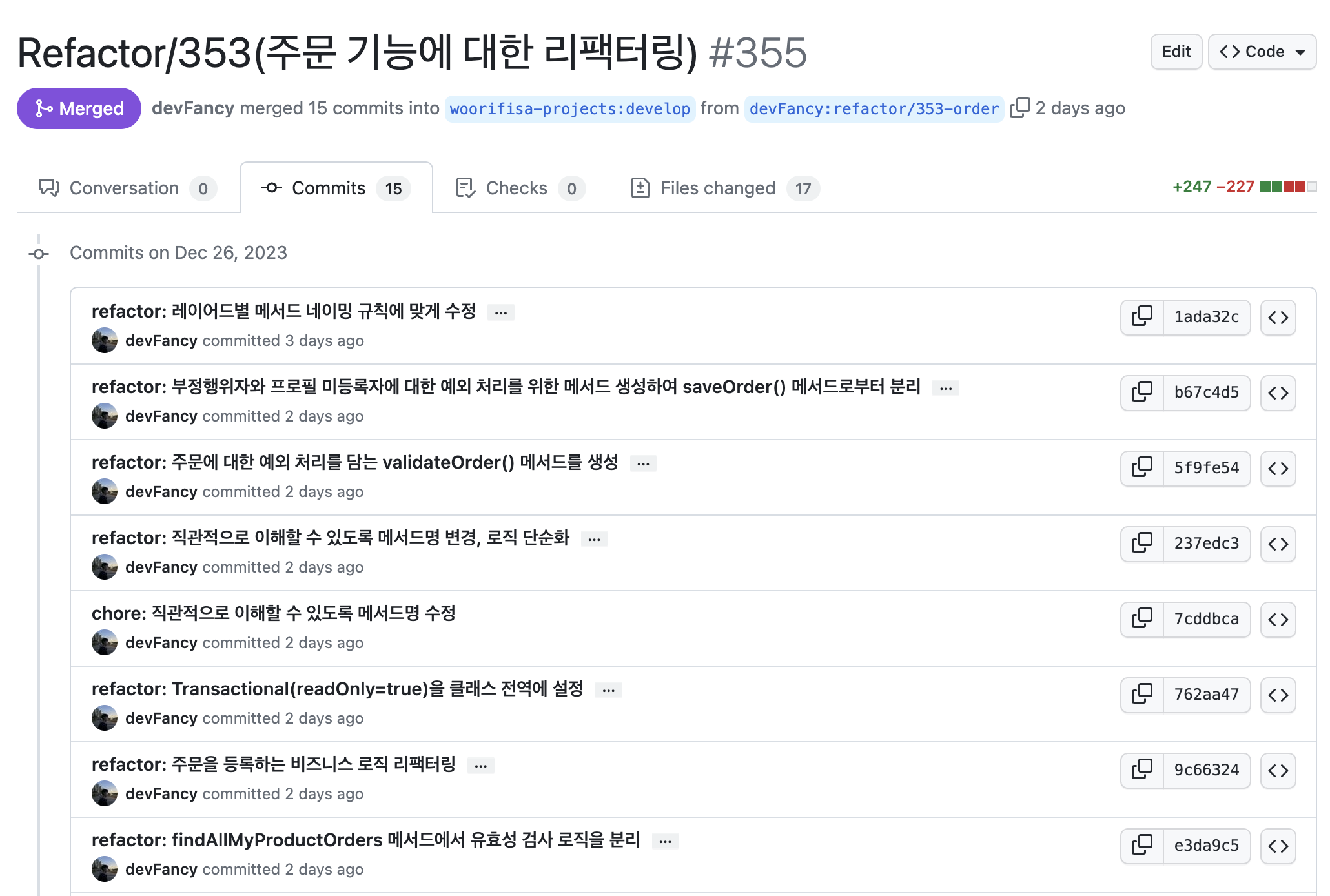
최근에
주문기능에 대해서 리팩터링 과정을 진행했는데, 작은 작업 단위 보다는 큰 작업으로 진행해서 아래와 같이 15개의 커밋 내용과 17개의 파일이 수정되었다.(물론, 10월 이후부터는 팀원들을 제외한 나 혼자만의 리팩터링을 진행해서 더 신경을 안쓴것도 맞다..ㅎㅎ 😅)
-
다음에 팀 프로젝트를 진행한다면,
커밋에 대해서도 신경쓰면서 작업을 진행하면 좋겠다는 생각이 들었다.(해당 영상을 참고하시면 더 자세하게 설명해주시니 참고하면 좋을 것 같습니다!)
Reference
-
[Programmers] SQL > JOIN 풀이 모음
상품 별 오프라인 매출 구하기(Lv.2)
-
문제:
PRODUCT테이블과OFFLINE_SALE테이블에서상품코드 별 매출액(판매가 * 판매량) 합계를 출력하는 SQL문을 작성해주세요.
결과는 매출액을 기준으로 내림차순 정렬해주시고
매출액이 같다면 상품코드를 기준으로 오름차순 정렬해주세요.
Answer Code 1 (23.12.27)
SELECT A.PRODUCT_CODE, (A.PRICE * B.TOT_SALES_AMOUNT) AS SALES FROM PRODUCT A LEFT JOIN ( SELECT PRODUCT_ID , SUM(SALES_AMOUNT) TOT_SALES_AMOUNT FROM OFFLINE_SALE B GROUP BY PRODUCT_ID ) B ON A.PRODUCT_ID = B.PRODUCT_ID ORDER BY SALES DESC, PRODUCT_CODE ASCAnswer Code1 - 문제 풀이
문제를 풀기 위해서 해야할 작업들
- OFFLINE_SALE 테이블에서 PRODUCT_ID별 판매 수량 집계하기(GROUP BY)
- PRODUCT 테이블과 조인하기(JOIN)
- 이때, 매출액은 상품코드 별 매출액(판매가 * 판매량) 합계를 계산(SUM)
- 매출액을 기준으로 내림차순 정렬, 만약 매출액이 같다면 상품코드를 기준으로 오름차순 정렬(ORDER BY)
-
첫 번째 단계는 OFFLINE_SALE 테이블에서 PRODUCT_ID 별 판매 수량을 집계한다.
-
이때 GROUP BY를 집계해서 각 상품별 수량을 산출한다.
SELECT PRODUCT_ID , SUM(SALES_AMOUNT) TOT_SALES_AMOUNT FROM OFFLINE_SALE B GROUP BY PRODUCT_ID-
두 번째 단계는 앞에서 진행한 결과를 서브쿼리로 넣고, PRODUCT 테이블을 기준으로 LEFT JOIN을 해준다.
-
이 결과를 통해 각 상품별 총 판매개수와 상품별 금액을 알 수 있다.
SELECT * FROM PRODUCT A LEFT JOIN ( SELECT PRODUCT_ID , SUM(SALES_AMOUNT) TOT_SALES_AMOUNT FROM OFFLINE_SALE B GROUP BY PRODUCT_ID ) B ON A.PRODUCT_ID = B.PRODUCT_ID- 세 번째 단계는 상품코드와 상품코드별 매출액(판매가 * 판매량) 합계를 산출한다.
SELECT A.PRODUCT_CODE, (A.PRICE * B.TOT_SALES_AMOUNT) AS SALES FROM PRODUCT A LEFT JOIN ( SELECT PRODUCT_ID , SUM(SALES_AMOUNT) TOT_SALES_AMOUNT FROM OFFLINE_SALE B GROUP BY PRODUCT_ID ) B ON A.PRODUCT_ID = B.PRODUCT_ID- 마지막 단계에서는 매출액을 기준으로 내림차순 정렬, 만약 매출액이 같다면 상품코드를 기준으로 오름차순 정렬(ORDER BY)을 해준다.
SELECT A.PRODUCT_CODE, (A.PRICE * B.TOT_SALES_AMOUNT) AS SALES FROM PRODUCT A LEFT JOIN ( SELECT PRODUCT_ID , SUM(SALES_AMOUNT) TOT_SALES_AMOUNT FROM OFFLINE_SALE B GROUP BY PRODUCT_ID ) B ON A.PRODUCT_ID = B.PRODUCT_ID ORDER BY SALES DESC, PRODUCT_CODE ASC
-
- DevHistory 4
- Essay 1
- Java 10
- Spring 15
- SpringBoot 17
- JPA 13
- MySQL 3
- Flyway 1
- Kafka 8
- Technology 22
- GoodCode 7
- Side_Project 20
- Retrospective 4
- AlgorithmSkill 3
- LeetCode 2
- Algorithm 70
- SQL 9
- OS 14
- Database 8
- Network 7
- HTTP 7
- DataStructure 5
- Linux 4
- Woowacourse 4
- Git 9
- AssertJ 1
- IntelliJ 5
- Probability-Statistics 5
- Electronic-Finance 13
- Business-Statistics 13
- Competition 1
- Book 6
- Workout 7
- E.T.C 8