지금의 기록이 미래의 자산이 된다.
Today's records become tomorrow's assets.-
[Goodfriends] - 사용자 기반 기능 전체 리팩터링
리팩터링을 도입하게 된 배경
-
8월 1일부터 9월 27일까지 팀 프로젝트를 진행했지만, 그 당시에는 ‘구현’에 초점이 맞춰졌기 때문에, 개개인의 코드의 품질에 제대로 신경쓰지 못하고 개발했다.
(초반에는 코드 리뷰를 열심히 해왔지만, 한정된 시간안에 구현해야 하는 압박감과 부담감에 후반으로 갈 수록 코드 리뷰를 제대로 못했다..)
그리고 좋은 코드가 무엇인지, 좋은 코드를 짜기 위해서 어떻게 리팩터링하는지에 대해서 제대로 알지 못했다.
-
그래서 팀 프로젝트가 끝난 이후에, ‘나중에 반드시 리팩터링 해야겠다!’ 고 다짐했다.
그렇게 한달이 지나고, 예상치 못한 좋은 기회로 11월부터 12월까지 우아한 스터디의 “
내 코드가 그렇게 이상한가요?” 주제에 참가하게 되어서, 좋은 코드가 무엇인지 배우게 되었다.“내 코드가 그렇게 이상한가요?” 책을 읽으면서 스터디에 참가하는 분들과 토론하면서 좋은 코드로 개선하는 방법을 알게되었다.
(해당 책을 공부하면서 내 블로그: GoodGode에 따로 정리해두었다)
-
해당 스터디에서 배운 내용을 기반으로 기존에 구현했던 기능들, 특히 사용자 기반 기능(프로필, 상품, 주문, 신고)을 우선적으로 리팩터링을 진행했다.
주문도메인에 대한 리팩터링 과정주요 기능 중 하나인
주문에 대한 리팩터링 과정을 자세히 확인하고 싶다면, PR을 참고하자.- 사용자 기반의 여러 기능 중
주문도메인에서 본인이 판매 등록한 물품에 들어온 주문서 전체를 조회하는 API와 관련된 비즈니스 로직에 대한 리팩터링 과정을 정리하고자 한다.
리팩터링 전)
주문도메인에서 주문서 전체를 조회하는 API에 대한 비즈니스 로직(OrderService.class) - findAllOrder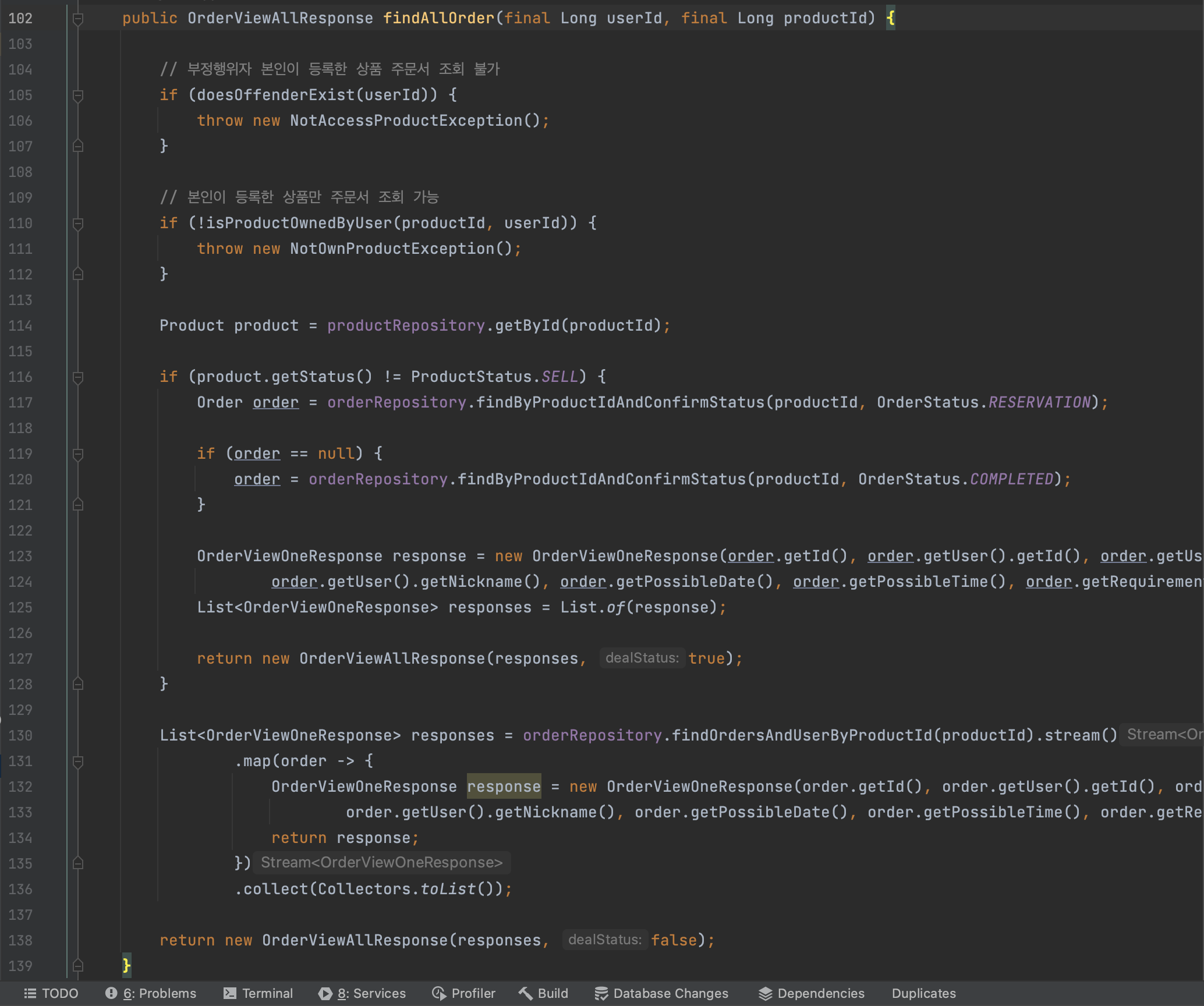
- 리팩터링을 하기전에, 지켜야할 부분을 아래와 같이 정리했다.
# 목표 - [ ] 구조를 파악할 수 있도록 기존의 클래스/메서드/변수명 수정할 것 - 굿프렌즈 WIKI에 있는 [객체 및 메서드 생성 규칙](https://github.com/woorifisa-projects/GoodFriends/wiki/객체-및-메서드-생성-규칙) - [ ] 불변 활용할 것 - [ ] 단일 책임 원칙을 지키기 위해 하나의 메서드에 한가지 일만 담당하도록 구현한다. - [ ] 메서드 최대 길이 15줄 이내로 할 것 - [ ] 리팩터링 이후 불필요한 주석은 제거할 것- [1] 먼저 구조를 파악할 수 있도록 기존의 클래스/메서드 변수명을 수정하기 위해
findAllOrder()메서드명을findAllMyProductOrders()로 수정했다.
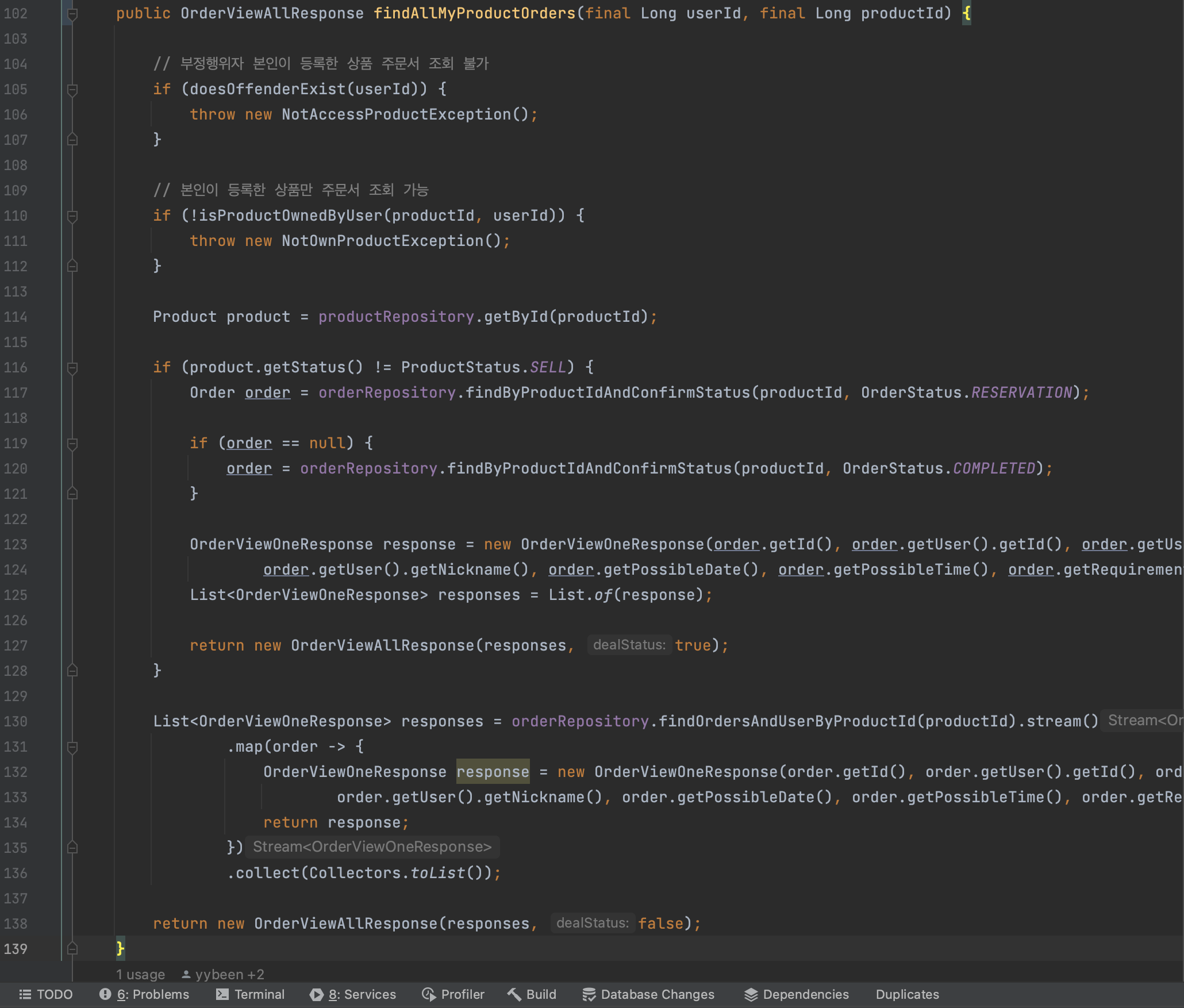
-
[2] 그리고
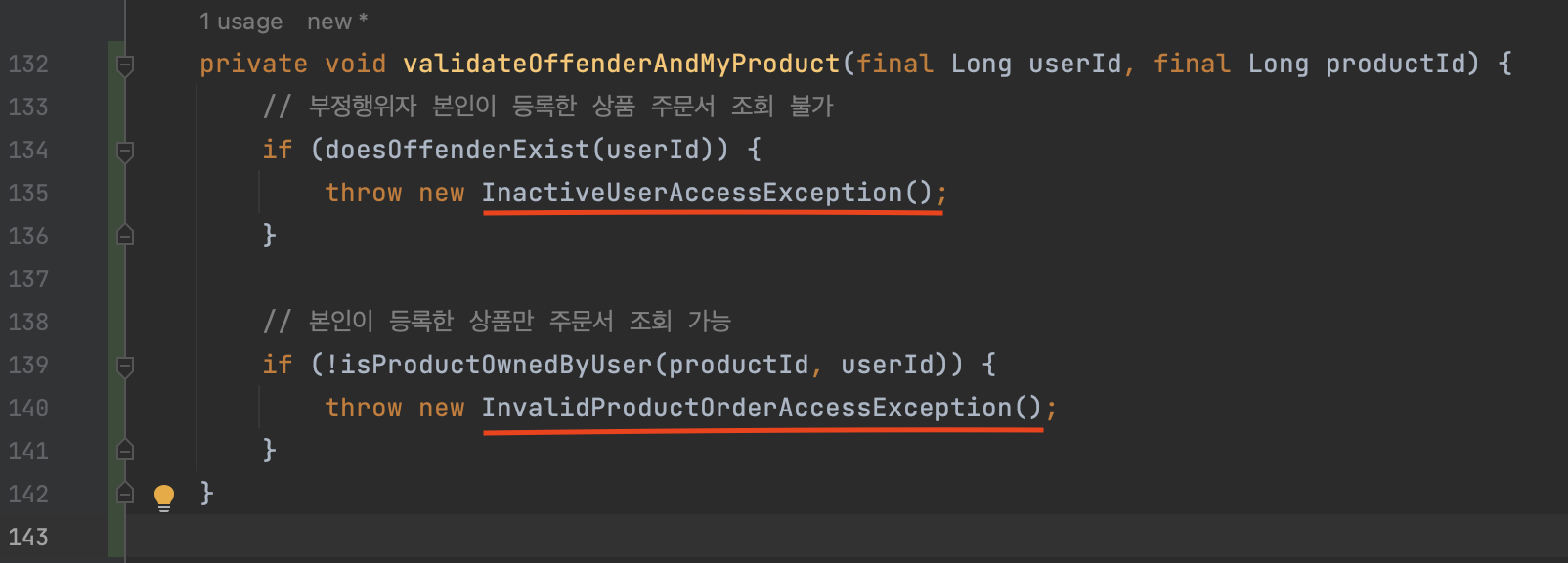
findAllMyProductOrders()메서드에서 유효성을 검사하는 로직을validateOffenderAndMyProduct()메서드를 생성해서 처리해주도록 수정했다. -
추가적으로 예외 클래스명에 대해서도 직관적이고 이해할 수 있는 클래스명으로 수정했다. (예외 처리 클래스를 각 도메인의 비즈니스 규칙에 맞도록 커스터마이징했다)
-
기존)
NotAccessProductException-> 변경)InactiveUserAccessException- 예외 메시지: ‘비활성화 상태인 유저로 해당 페이지에 접근이 불가능합니다’ -
기존)
NotOwnProductException-> 변경)InvalidProductOrderAccessException- 예외 메시지: ‘본인이 등록하지 않은 상품의 주문서는 조회할 수 없습니다.’
-
-
[3]
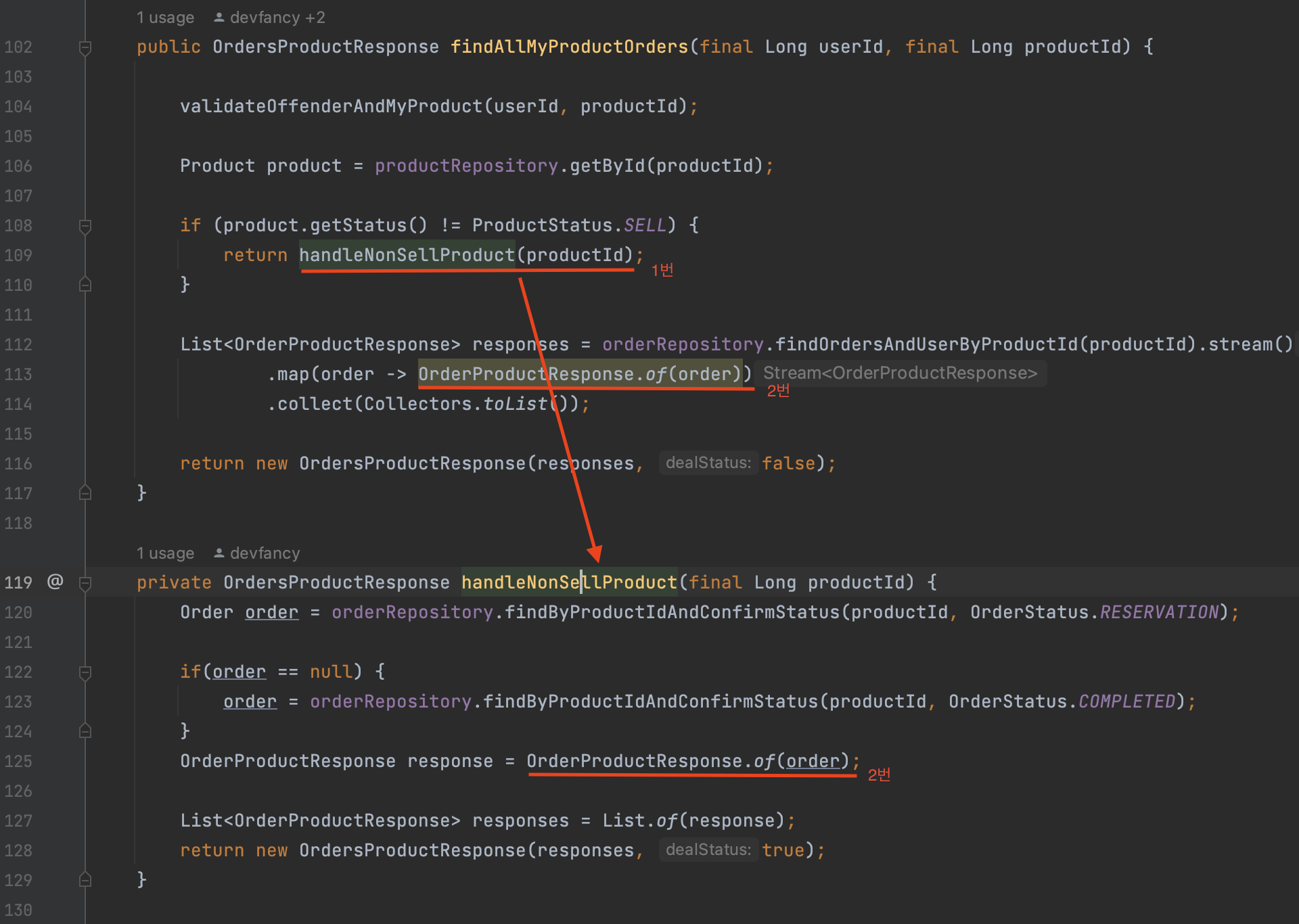
findAllMyProductOrders()에는 여러 로직을 처리하고 있어서단일 책임 원칙에 위배되고 있다. -
이를 해결하기 위해 첫 번째로 하나의 메서드에 한 가지 일만 담당하도록 로직을 수정했고, 동시에 중첩 if문을 제거했다.
- 이때, 상태 체크와 해당 상태에 따른 주문서를 조회하는 로직을 분리했다. ->
handleNonSellProduct()
- 이때, 상태 체크와 해당 상태에 따른 주문서를 조회하는 로직을 분리했다. ->
-
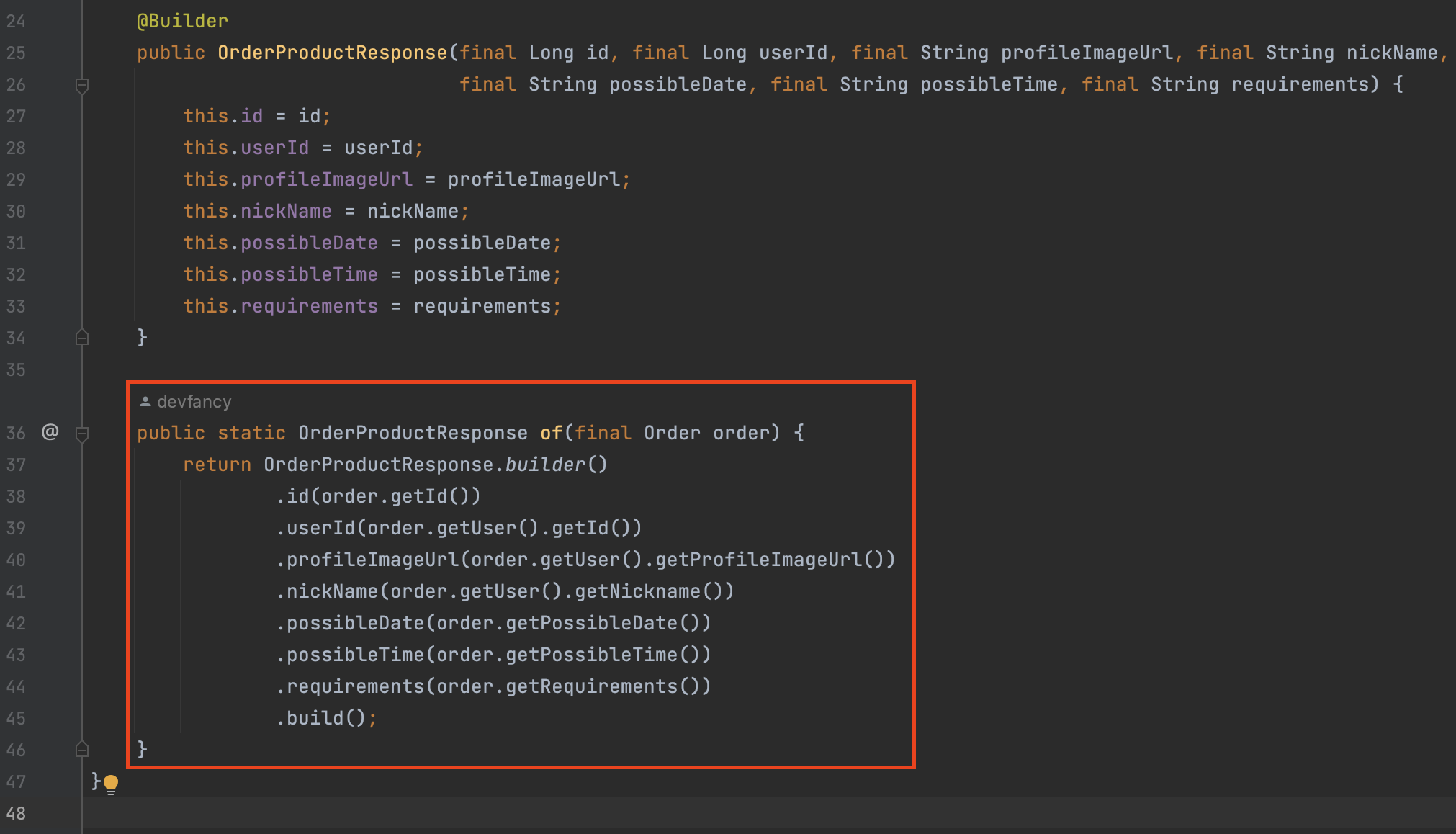
[4] 그런 다음, 두 번째로 map 부분에서
OrderProductResponse클래스(이전 클래스명:OrderViewOneResponse)정적 팩토리 메서드(of)를 추가하여 중복되는 부분을 최소화했다.-
팩토리 메서드 패턴(Factory Method Pattern)은 객체 생성을 처리하기 위한 디자인 패턴 중 하나다. -
이 패턴을 사용함으로써 객체 생성과정이 클래스 외부로 추상화되어, 코드의 가독성이 높아지고 유지보수가 용이해진다.
-
또한
팩토리 메서드 패턴은 객체 생성에 필요한 복잡한 로직을 한 곳에 모아둠으로써 중복을 줄일 수 있다. -
of메서드는 주로 정적(static) 팩터리 메서드로 사용되며, 해당 객체를 생성하고 초기화하는데 사용된다. 불변성(Immutability)을 강조하거나 특정한 시나리오에서 명확하게 사용할 수 있도록 하는데 주로 쓰인다.
-
- [5]
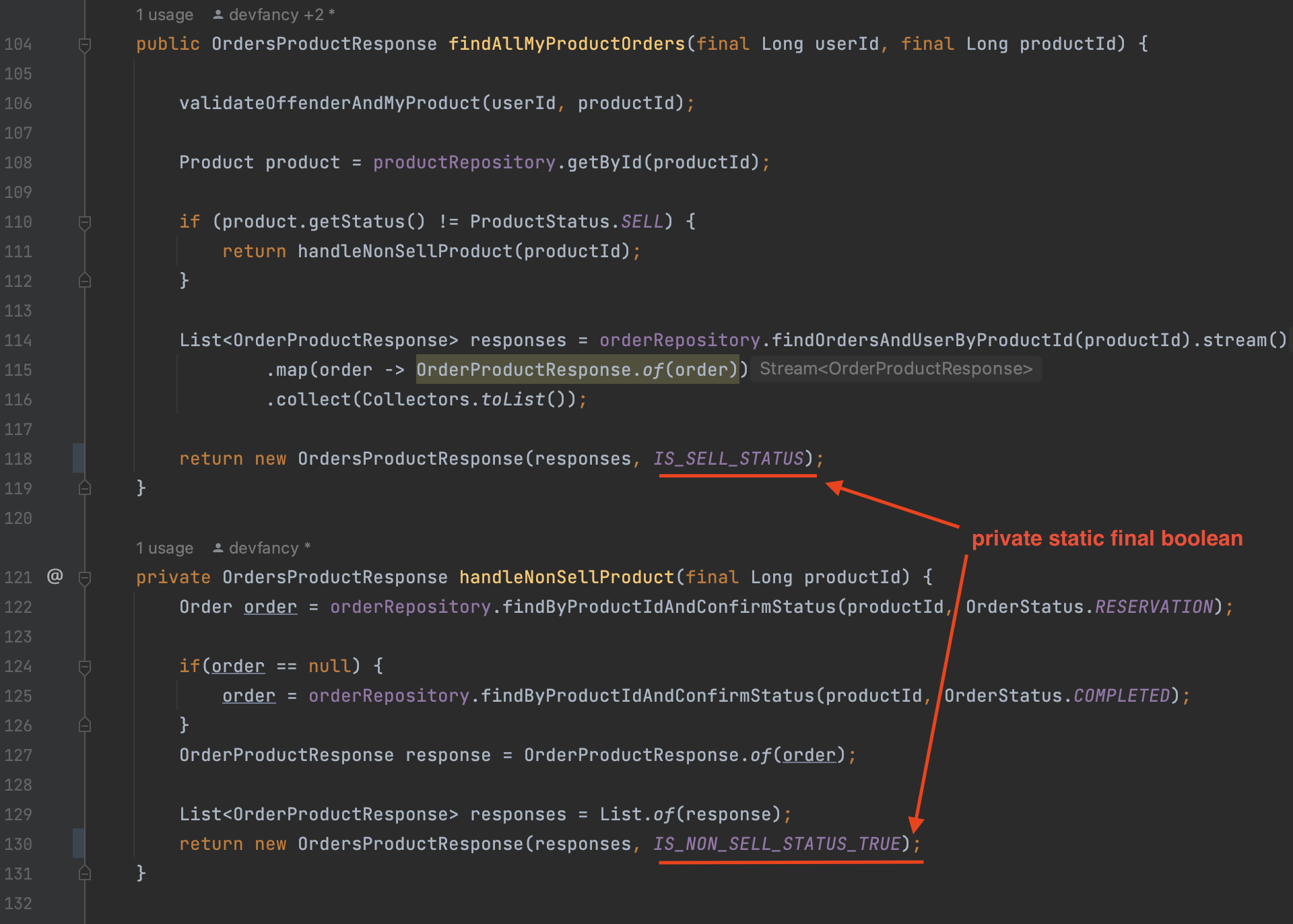
findAllMyProductOrders(),handleNonSellProduct()두 메서드의 return 하는 부분에서 true/false 값은 판매 상태 여부를 나타내는 걸 의미하는데, 이를private static final로 상수화로 선언해서 아래와 같이 수정했다.
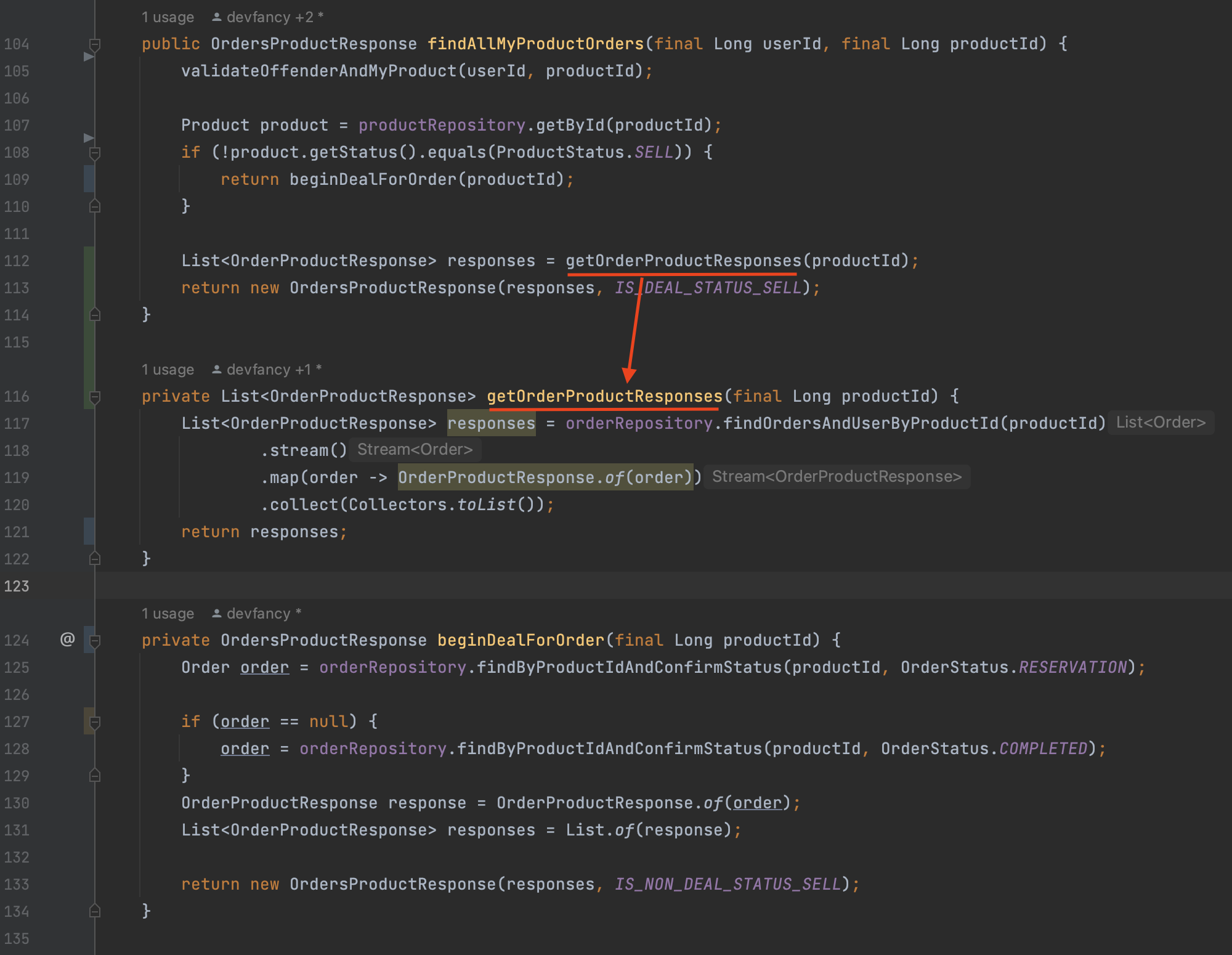
- [6]
findAllMyProductOrders()메서드에서 주문 응답을 가져오는 로직을getOrderProductResponses()메서드로 추출했다.
-
마지막으로
findAllMyProductOrders()메서드에서 로직을 처리하는 순서에 맞게 조정했다.그리고
handleNonSellProduct()메서드 명에 대해서도 직관적으로 이해할 수 있게beginDealForOrder()으로 다시 수정했다. -
이렇게 해서
주문도메인에서 본인이 판매 등록한 물품에 들어온 주문서 전체를 조회하는 API와 관련된 비즈니스 로직에 대한 리팩터링을 진행했다.
# 목표 달성 - [x] 구조를 파악할 수 있도록 기존의 클래스/메서드/변수명 수정할 것 - 굿프렌즈 WIKI에 있는 [객체 및 메서드 생성 규칙](https://github.com/woorifisa-projects/GoodFriends/wiki/객체-및-메서드-생성-규칙) - [x] 불변 활용할 것 - [x] 단일 책임 원칙을 지키기 위해 하나의 메서드에 한가지 일만 담당하도록 구현한다. - [x] 메서드 최대 길이 15줄 이내로 할 것 - [x] 리팩터링 이후 불필요한 주석은 제거할 것리팩터링 후)
주문도메인에서 주문서 전체를 조회하는 API에 대한 비즈니스 로직(OrderService.class) -findAllMyProductOrders()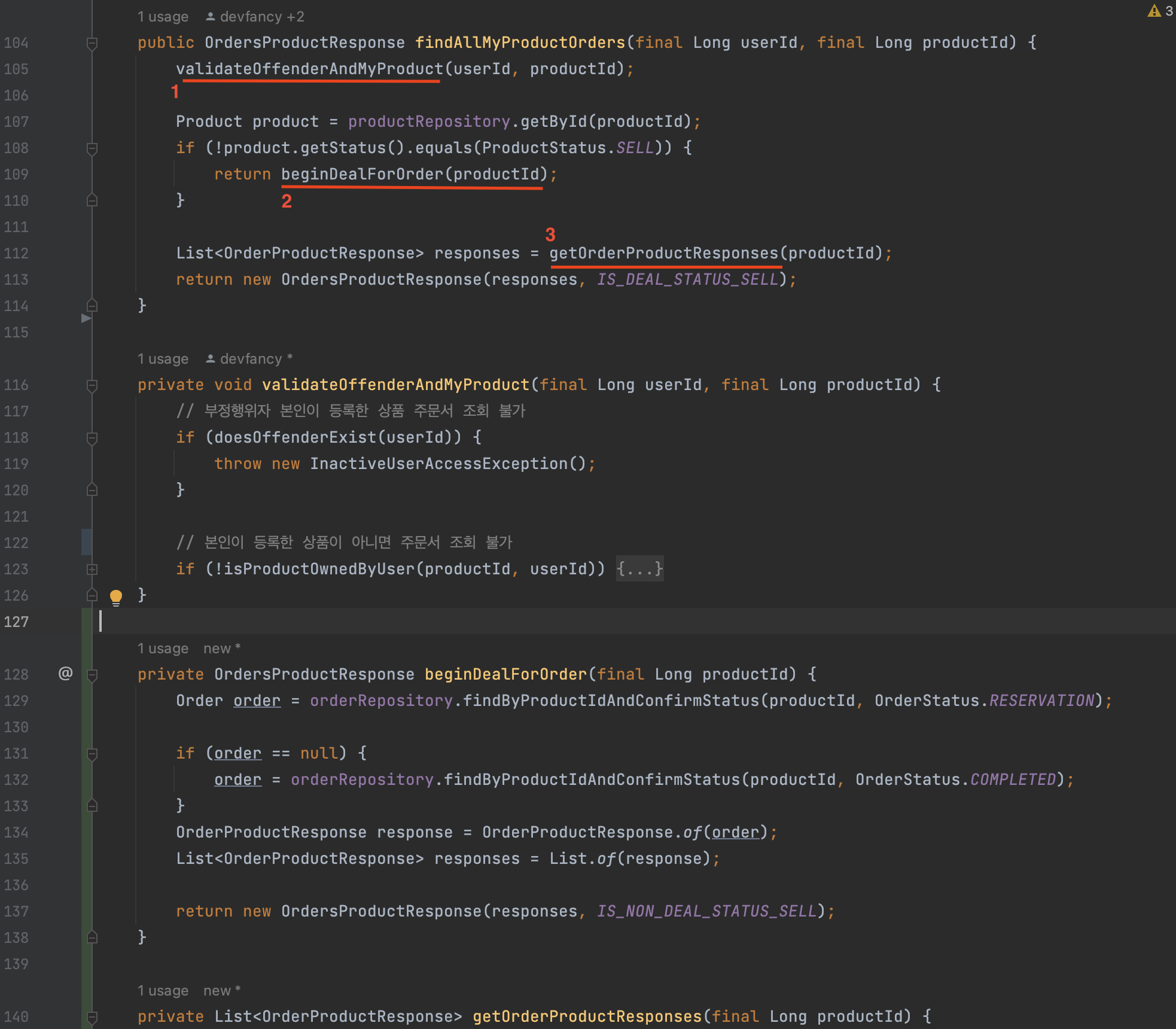
리팩터링을 마치며
-
사실
주문도메인에 대한 리팩터링 하기 이전에, 이미프로필,신고,상품에 대해 리팩터링을 진행했다. -
스터디에서 배운 내용을 기반으로 기존 프로젝트(굿프렌즈)에서 사용자 기반의 기능들을 모두 리팩터링하면서 적용해봤다.
-
책에 있는 기술, 개념들을 적용하는 과정에서 시간이 많이 걸렸지만, 그 만큼 많은 경험을 얻게 되었다.
-
다음에는 이전에 테스트 코드 강의를 듣고 정리해둔 Practical Testing: 테스트 코드 작성 방법을 기반으로 굿프렌즈 프로젝트에 단위 및 통합 테스트 코드를 작성해보자!
-
-
[Programmers] SQL > String, Date 풀이 모음
- 자동차 대여 기록에서 장기/단기 대여 구분하기(Lv.1)
- 특정 옵션이 포함된 자동차 리스트 구하기(Lv.1)
- 조건에 부합하는 중고거래 상태 조회하기(Lv 2)
- 조건에 맞는 사용자 정보 조회하기(Lv.3)
- 조회수가 가장 높은 중고거래 게시물에 대한 첨부파일 경로를 조회하기(Lv.3)
- 조건별로 분류하여 주문상태 출력하기(Lv 3)
자동차 대여 기록에서 장기/단기 대여 구분하기(Lv.1)
-
문제:
CAR_RENTAL_COMPANY_RENTAL_HISTORY테이블에서 대여 시작일이2022년 9월에 속하는 대여 기록에 대해서 대여 기간이 30일 이상이면 ‘장기 대여’
그렇지 않으면 ‘단기 대여’ 로 표시하는 컬럼(컬럼명: RENT_TYPE)을 추가하여
대여기록을 출력하는 SQL문을 작성해주세요.
결과는 대여 기록 ID를 기준으로 내림차순 정렬해주세요.
Answer Code(2023.12.22)
SELECT HISTORY_ID, CAR_ID, DATE_FORMAT(START_DATE, '%Y-%m-%d') AS START_DATE, DATE_FORMAT(END_DATE, '%Y-%m-%d') AS END_DATE, CASE WHEN DATEDIFF(END_DATE, START_DATE) + 1 >= 30 THEN "장기 대여" ELSE "단기 대여" END AS RENT_TYPE FROM CAR_RENTAL_COMPANY_RENTAL_HISTORY WHERE START_DATE BETWEEN '2022-09-01' AND '2022-09-30' ORDER BY HISTORY_ID DESC;문제 풀이
문제를 풀기 위해서 해야할 작업들
- 대여시작일이 2022년 9월인 기옥에 대해서 대여 기간이 30일 이상인 경우 “장기 대여” 그렇지 않으면 “단기 대여”로 구분(
RENT_TYPE컬럼 추가) - 데이터 포맷은 예시와 동일하게 나타내기
대여 기옥 ID를 기준으로 내림차순하기
DATE_FORMAT: MySQL에서 사용되는 날짜 데이터의 출력 형식을 지정하는 함수-
DATE_FORMAT(START_DATE, '%Y-%m-%d')은 start_date 에서'%Y-%m-%d'형식으로 반환해준다.(대부분의 날짜 데이터는
%Y-%m-%d형식을 많이 사용한다.) -
%Y: 4자리 연도(예: 2023) /%y: 2자리 연도 (예: 23) -
%m: 월 (01부터 12까지) -
%d: 일 (01부터 31까지)
DATEDIFF: MySQL에서 사용되는 두 날짜 간의 차이를 계산하는 함수-
이 함수는 첫 번째 날짜에서 두 번째 날짜를 뺀 결과를 반환해준다.
-
기본 사용 형식:
DATEDIFF(END_DATE, START_DATE) -
중요) 오늘 대여하고 오늘 반납해도 대여 기간은 하루 기간이기 때문에, (END_DATE - START_DATE) +1 >= 30 으로 계산해야 한다.
# 대여기간 예시 2023년 12월 22일 대여 >> 2023년 12월 22일 반납: 1일 = (22 - 22)일 + 1일 = 1일 2023년 12월 22일 대여 >> 2023년 12월 23일 반납: 2일 = (23 - 22)일 + 1일 = 2일CASE 문: 조건에 따라 새로운 값을 부여하여 새로운 컬럼을 부여하는 경우에 사용한다.- 아래는
CASE 문의 기본 사용 형식이다.
CASE WHEN 조건 1 THEN 조건 1 만족 시 반환하는 값 WHEN 조건 2 THEN 조건 2 만족 시 반환하는 값 ELSE 조건들에 만족 안 하는 경우 반환 값 END특정 옵션이 포함된 자동차 리스트 구하기(Lv.1)
-
문제:
CAR_RENTAL_COMPANY_CAR테이블에서 ‘네비게이션’ 옵션이 포함된 자동차 리스트를 출력하는 SQL문을 작성해주세요.결과는 자동차 ID를 기준으로 내림차순 정렬해주세요.
Answer Code1
select car_id, car_type, daily_fee, options from car_rental_company_car where options like '%네비게이션%' order by car_id desc문제 풀이
문제를 풀기 위해서 해야할 작업들
네비게이션옵션이 포함된 자동차 리스트를 출력한다.- 자동차 ID를 기준으로 내림차순으로 정렬한다.
-
CAR_RENTAL_COMPANY_CAR테이블에서 ‘네비게이션’ 옵션이 포함 => where + like 절을 사용한다. =>like '%네비게이션%' -
order by car_id desc=>DESC는 내림차순(ASC는 오름차순 이다)
조건에 부합하는 중고거래 상태 조회하기(Lv 2)
-
문제:
USED_GOODS_BOARD테이블에서 2022년 10월 5일에 등록된중고거래 게시물의 게시글 ID, 작성자 ID, 게시글 제목, 가격, 거래상태를 조회하는 SQL문을 작성해주세요.
거래상태가 SALE 이면 판매중, RESERVED이면 예약중, DONE이면 거래완료 분류하여 출력해주시고,
결과는 게시글 ID를 기준으로 내림차순 정렬해주세요.
Answer Code
SELECT BOARD_ID, WRITER_ID, TITLE, PRICE, CASE WHEN STATUS = 'SALE' THEN '판매중' WHEN STATUS = 'RESERVED' THEN '예약중' WHEN STATUS = 'DONE' THEN '거래완료' END STATUS FROM USED_GOODS_BOARD WHERE BOARD_ID IN( SELECT BOARD_ID FROM USED_GOODS_BOARD WHERE CREATED_DATE = '2022-10-05' ) ORDER BY BOARD_ID DESC;문제 풀이
문제를 풀기 위해서 해야할 작업들
- 2022년 10월 5일에 등록된 중고 거래 게시물에서 (WHERE)
- 필요한 컬럼들 조회(SELECT)
- 거래 상태에 따라 분류해서 출력(CASE)
- 게시글 ID를 기준으로 내림차순 정렬(ORDER BY)
조건에 맞는 사용자 정보 조회하기(Lv.3)
-
문제:
USED_GOODS_BOARD와USED_GOODS_USER테이블에서중고 거래 게시물을 3건 이상 등록한 사용자의 사용자 ID, 닉네임, 전체주소, 전화번호를 조회하는 SQL문을 작성해주세요.
이때, 전체 주소는 시, 도로명 주소, 상세 주소가 함께 출력되도록 해주시고,
전화번호의 경우
xxx-xxxx-xxxx같은 형태로 하이픈 문자열(-)을 삽입하여 출력해주세요.결과는 회원 ID를 기준으로 내림차순 정렬해주세요.
Answer Code
select user.user_id, user.nickname, concat(user.city,' ', user.street_address1,' ', user.street_address2) AS 전체주소, concat(LEFT(tlno, 3), '-', MID(tlno, 4, 4),'-', RIGHT(tlno, 4)) AS 전화번호 from used_goods_user as user join used_goods_board as board on user.user_id = board.writer_id group by board.writer_id having count(board.writer_id) >= 3 order by user.user_id desc;문제 풀이
문제를 풀기 위해서 해야할 작업들
USED_GOODS_BOARD테이블에서 writer_id 컬럼의 값을 count하여 3개 이상인 writer_id 찾기- CONCAT() 함수와
USED_GOODS_USER의 CITY, STREET_ADDRESS1, STREET_ADDRESS2를 활용하여 ‘전체주소’ 생성하기 - CONCAT() 함수와
USED_GOODS_USER의 TLNO를 활용하여 ‘전화번호’ 생성하기 - USER_ID 기준으로 내림차순하기
GROUP BY구문: 주로 집계 함수(COUNT)와 함께 사용되어 특정 열의 값에 기반하여 그룹을 형성하는 역할group by board.writer_id having count(board.writer_id) >= 3-
USER_GOODS_BOARD테이블에서WRITER_ID열을 기준으로 그룹을 형성한다. -
그런 다음,
HAVING구문을 사용하여USER_GOOD_BOARD테이블에서 각 작성자(WRITER_ID)가 최소 3개 이상의 게시물을 작성한 경우에만 해당 그룹이 선택된다.
CONCAT()함수: SQL에서 사용되는 문자열을 연결하는 함수concat(user.city,' ', user.street_address1,' ', user.street_address2) AS 전체주소-
SELECT 절에서 “CONCAT() 함수”를 이용해서
CITY,STREET_ADDRESS1,STREET_ADDRESS2컬럼을 하나의 문자열로 연결하는 작업이다. -
예시에서 나온 것과 같게 만들기 위해서는 공백(‘ ‘)으로 각 컬럼의 값을 구분하고, AS 절을 이용하여 요구한 컬럼의 이름과 동일하게
전체주소라는 컬럼을 부여했다.
concat(LEFT(tlno, 3), '-', MID(tlno, 4, 4),'-', RIGHT(tlno, 4)) AS 전화번호-
“CONCAT() 함수”를 이용해서 연결 사이에 ‘-‘ 으로 구분하여 하나의 문자열을 만들었다.
-
LEFT(tlno, 3): 전화번호 문자열의 왼쪽에서 3자리를 추출
-
MID(tlno, 4, 4): 전화번호 문자열에서 4번째 위치에서부터 4자리를 추출
-
RIGHT(tlno, 4): 전화번호 문자열의 오른쪽에서 4자리를 추출합니다.
-
다른 방법: SUBSTR((또는 SUBSTRING)) 함수 사용 : 문자열에서 일부분을 추출하는 데 사용되는 SQL 함수이다.
CONCAT(SUBSTR(TLNO, 1, 3), '-', SUBSTR(TLNO, 4, 4), '-', SUBSTR(TLNO, 8)) AS 전화번호-
일반적인 사용 형식:
SUBSTR(string, start_position, length)-
string: 추출하려는 문자열
-
start_position: 추출을 시작할 위치입니다. 1부터 시작한다.
-
length (선택사항): 추출하려는 부분의 길이를 지정한다. 만약 이 부분을 생략하면 시작 위치부터 문자열의 끝까지 추출하게 된다.
-
-
SUBSTR()(또는 SUBSTRING) 함수: 문자열에서 일부분을 추출하는 데 사용되는 SQL 함수이다.-
SUBSTR(TLNO, 1, 3): 전화번호 문자열의 1번째 위치에서부터 3자리를 추출
-
SUBSTR(TLNO, 4, 4): 전화번호 문자열에서 4번째 위치에서부터 4자리를 추출
-
SUBSTR(TLNO, 8): 전화번호 문자열의 8번째 위치에서부터 끝까지 추출
-
Answer Code2
SELECT USER_ID , NICKNAME , CONCAT(CITY, ' ', STREET_ADDRESS1, ' ', STREET_ADDRESS2) AS '전체주소' , CONCAT(SUBSTR(TLNO, 1, 3), '-', SUBSTR(TLNO, 4, 4), '-', SUBSTR(TLNO, 8)) AS '전화번호' FROM USED_GOODS_USER WHERE USER_ID IN ( SELECT WRITER_ID FROM USED_GOODS_BOARD GROUP BY WRITER_ID HAVING COUNT(*) >= 3 ) ORDER BY USER_ID DESC;문제 풀이
-
위 정답은 다른 사람이 푼 것을 가져와봤다.
-
Answer Code1는 join을 사용했는데,Answer Code2는 join 없이 서브 쿼리를 사용한 SQL 구문이다.
조회수가 가장 높은 중고거래 게시물에 대한 첨부파일 경로를 조회하기(Lv.3)
-
문제:
USED_GOODS_BOARD와USED_GOODS_FILE테이블에서조회수가 가장 높은 중고거래 게시물에 대한 첨부파일 경로를 조회하는 SQL문을 작성해주세요.
첨부파일 경로는 FILE ID를 기준으로 내림차순 정렬해주세요.
기본적인 파일경로는 /home/grep/src/ 이며, 게시글 ID를 기준으로 디렉토리가 구분되고,
파일이름은 파일 ID, 파일 이름, 파일 확장자로 구성되도록 출력해주세요.
조회수가 가장 높은 게시물은 하나만 존재합니다.
Answer Code1
SELECT CONCAT('/home/grep/src/', BOARD_ID, '/', FILE_ID, FILE_NAME, FILE_EXT) AS FILE_PATH FROM USED_GOODS_FILE WHERE BOARD_ID = ( SELECT BOARD_ID FROM USED_GOODS_BOARD ORDER BY VIEWS DESC LIMIT 1 ) ORDER BY FILE_ID DESC;문제 풀이
문제를 풀기 위해서 해야할 작업들
- CONCAT() 함수를 이용하여
USED_GOODS_FILE테이블에서 BOARD_ID 를 기준으로 디렉터리를 ‘/’ 으로 구분하고, 파일이름은 FILE_ID, FILE_NAME, FILE_EXT로 구성되도록 한다. - 조건 WHERE 절에서
USED_GOODS_BOARD테이블에서 가장 높은 조회수(VIEW)를 SELECT 절과 MAX를 이용해서 하나만 조회하도록 한다. - FILE_ID를 기준으로 내림차순 정렬하여 결과를 출력한다.
[1]. CONCAT() 함수를 이용하여
USED_GOODS_FILE테이블에서 BOARD_ID 를 기준으로 디렉터리를 ‘/’ 으로 구분하고, 파일이름은 FILE_ID, FILE_NAME, FILE_EXT로 구성되도록 한다.SELECT CONCAT('/home/grep/src/', BOARD_ID, '/', FILE_ID, FILE_NAME, FILE_EXT) AS FILE_PATH FROM USED_GOODS_FILE[2]. 조건 where 절에서
USED_GOODS_BOARD테이블에서 가장 높은 조회수(VIEW)를 SELECT 절과 ORDER BY, LIMIT절을 이용해서 하나만 조회한다.WHERE BOARD_ID = ( SELECT BOARD_ID FROM USED_GOODS_BOARD ORDER BY VIEWS DESC LIMIT 1 )[3]. FILE_ID를 기준으로 내림차순 정렬하여 결과를 출력한다.
ORDER BY FILE_ID DESC;Answer Code2
SELECT CONCAT('/home/grep/src/', FILE.BOARD_ID, '/', FILE_ID, FILE_NAME, FILE_EXT) AS FILE_PATH FROM USED_GOODS_FILE AS FILE LEFT JOIN USED_GOODS_BOARD AS BOARD ON FILE.BOARD_ID = BOARD.BOARD_ID WHERE VIEWS = (SELECT MAX(VIEWS) FROM USED_GOODS_BOARD) ORDER BY FILE_ID DESC조건별로 분류하여 주문상태 출력하기(Lv 3)
-
문제:
FOOD_ORDER테이블에서 5월 1일을 기준으로 주문 ID, 제품 ID, 출고일자, 출고여부를 조회하는 SQL문을 작성해주세요.출고여부는 5월 1일까지 출고완료로 이 후 날짜는 출고 대기로 미정이면 출고미정으로 출력해주시고,
결과는 주문 ID를 기준으로 오름차순 정렬해주세요.
Answer Cod(2023.12.26)
SELECT ORDER_ID, PRODUCT_ID, DATE_FORMAT(OUT_DATE, '%Y-%m-%d') as OUT_DATE, case when OUT_DATE <= '2022-05-01' then '출고완료' when OUT_DATE > '2022-05-01' then '출고대기' else '출고미정' end '출고여부' from FOOD_ORDER order by ORDER_ID asc;
-
[Programmers] 159993. 미로탈출 (BFS)
성능 요약
-
메모리: 78.4 MB, 시간: 0.56 ms - 23.10.24
-
메모리: 82.6 MB, 시간: 0.35 ms - 23.12.16
구분
- 코딩테스트 연습 > 연습문제 > 미로탈출(BFS)
Answer Code1(23.10.24)
import java.util.*; class Solution { static int[] dRow = {-1, 1, 0, 0}; // 행 기준 - 상,하,좌,우 (좌우로의 이동은 y좌표에 변화가 없으므로 0) static int[] dCol = {0, 0, -1, 1}; // 열 기준 - 상,하,좌,우 (상하로의 이동은 x좌표에 변화가 없으므로 0) static int[] lever = new int[2]; public int solution(String[] maps) { int answer = 0; // 탐색을 위한 2차원 배열과 방문 배열 초기화 String[][] map = new String[maps.length][maps[0].length()]; boolean[][] visited = new boolean[maps.length][maps[0].length()]; int[] start = new int[2]; // 2차원 배열을 만들며 최초 시작 위치 탐색 for(int i = 0; i < maps.length; i++) { String[] temp = maps[i].split(""); map[i] = temp; for(int j = 0; j < temp.length; j++) { if(temp[j].equals("S")) { start[0] = i; start[1] = j; } } } // 레버까지 BFS 탐색 int first = bfs(map, visited, start, "L"); if(first == -1) { return -1; } // 탈출지점까지 BFS 탐색 visited = new boolean[maps.length][maps[0].length()]; int second = bfs(map, visited, lever, "E"); if(second == -1) { return -1; } answer = first + second; return answer; } public int bfs(String[][] map, boolean[][] visited, int[] start, String target) { Queue<int[]> queue = new LinkedList<>(); queue.add(new int[]{start[0], start[1], 0}); // 현재 행, 현재 열, 이동 횟수 visited[start[0]][start[1]] = true; while(!queue.isEmpty()) { int[] temp = queue.poll(); int currentRow = temp[0]; int currentCol = temp[1]; int cnt = temp[2]; for(int i = 0; i < 4; i++) { int newRow = currentRow + dRow[i]; int newCol = currentCol + dCol[i]; if(newRow >= 0 && newRow < map.length && newCol >= 0 && newCol < map[0].length) { if(map[newRow][newCol].equals(target)) { lever[0] = newRow; lever[1] = newCol; return cnt + 1; } if(!map[newRow][newCol].equals("X") && !visited[newRow][newCol]) { visited[newRow][newCol] = true; queue.add(new int[]{newRow, newCol, cnt + 1}); } } } } return -1; } }Answer Code2(23.12.16)
import java.util.*; import java.io.*; // 미로탈출 class Solution { static int[] dRow = {-1, 1, 0, 0}; static int[] dCol = {0, 0, -1, 1}; static int[] lever = new int[2]; public int bfs(String[][] map, boolean[][] visited, int[] start, String target) { visited[start[0]][start[1]] = true; Queue<int[]> queue = new LinkedList<>(); // 현재 행, 현재 열, 이동 횟수 queue.add(new int[]{start[0], start[1], 0}); while (!queue.isEmpty()) { int[] temp = queue.poll(); int curRow = temp[0]; int curCol = temp[1]; int count = temp[2]; for(int i = 0; i < 4; i++) { int nextRow = curRow + dRow[i]; int nextCol = curCol + dCol[i]; if(nextRow >= 0 && nextRow < map.length && nextCol >= 0 && nextCol < map[0].length) { if(map[nextRow][nextCol].equals(target)) { lever[0] = nextRow; lever[1] = nextCol; return count + 1; } if(!map[nextRow][nextCol].equals("X") && visited[nextRow][nextCol] == false) { visited[nextRow][nextCol] = true; queue.add(new int[]{nextRow, nextCol, count + 1}); } } } } return -1; } public int solution(String[] maps) { // 0. 입력 및 초기화 int answer = 0; String[][] map = new String[maps.length][maps[0].length()]; boolean[][] visited = new boolean[maps.length][maps[0].length()]; for(int i = 0; i < maps.length; i++) { for(int j = 0; j < maps[0].length(); j++) { visited[i][j] = false; } } int[] start = new int[2]; // 1. 연결정보 채우기 - 2차원 배열을 만들며 최초 시작 위치 탐색 후 저장 for(int i = 0; i < maps.length; i++) { String[] temp = maps[i].split(""); map[i] = temp; for(int j = 0; j < temp.length; j++) { if(temp[j].equals("S")) { start[0] = i; start[1] = j; } } } // 2-1. 레버까지 BFS 탐색 int first = bfs(map, visited, start, "L"); if(first == -1) { // 만약 레버를 발견하지 못했다면 -1을 return return -1; } // 2-2. 탈출 지점까지 BFS 탐색 visited = new boolean[maps.length][maps[0].length()]; int second = bfs(map, visited, lever, "E"); // 3. 출력하기 if(second == -1 ) { // 만약 탈출할 수 없다면 -1을 return return -1; } answer = first + second; return answer; } }문제 풀이(Answer Code1,2)
문제 요약
- 벽으로 된 칸은 지나갈 수 X, 통로로 된 칸만 이동 가능
- 통로들 중 한 칸에는 미로를 빠져나가는 문이 있음 -> 이 문은 레버를 당겨서만 열 수 있음
- 레버가 있는 칸으로 이동 -> 레버를 당긴 후 미로를 빠져나가는 문이 있는 칸으로 이동
- 레버를 당기지 않았더라도 출구가 있는 칸을 지나갈 수 있음
- 결론은 주어진 미로에서 시작점(S)로 부터 레버(L)을 당기고 다시 탈출구(E)를 도달하는데 최단 거리를 구하는 문제다.
로직 구성
- 먼저 탈출을 하기 위해서는 레버까지 가야한다.
- 레버까지 BFS를 통해 최단거리 탐색을 진행한다.
- 레버에 도착하고 다시 한번 탈출지점까지 BFS 탐색을 한다.
- 탈출 조건이 (시작 지점에서 레버에 도달 && 레버에서 탈출 지점까지 도달) 할때의 최소 시간을 return 해주고,
- 이러한 조건이 만족하지 못하면 -1를 return 한다.
Review
23.12.16
-
GPT가 “일반적으로 BFS가
미로,최단 경로등을 찾는 데에 더 적합한 알고리즘이기 때문에 BFS를 선호합니다.” 라고 해서- BFS로 다시 풀었는데, 레버까지 가는 것과 탈출지점까지 가는 것을 분리해서 접근해서 풀었다.
-
추가적으로 GPT에게 DFS와 BFS에 어떤 유형이 적합하는지 물어봤다.
-
DFS는 주로 트리나 그래프에 사용해서 특정 경로를 탐색하는 경우 적합하고, -
BFS는 최단 경로를 찾거나 인접한 노드들을 탐색하는 경우에 적합하다고 답변했다.
-
-
지난 3주동안
DFS기반으로 문제를 풀어서BFS로 문제를 푸는 방식이 아직 서툴지만,문제유형에 맞게 두가지 접근 방식을 계속적으로 사용해서 익숙해지자!
Reference
-
-
[Programmers] 1844. 게임 맵 최단거리(bfs)
성능 요약
- 메모리: 68.8 MB, 시간: 4.79 ms
구분
- 코딩테스트 연습 > 깊이/너비 우선 탐색(DFS/BFS)
Answer Code1(2023.02.14)
import java.util.*; class Solution { public class position { int x; int y; public position(int x, int y) { this.x = x; this.y = y; } } int[] nx = {-1, 1, 0, 0}; int[] ny = {0, 0, -1, 1}; public int solution(int[][] maps) { int h = maps.length; int w = maps[0].length; Queue<position> q = new LinkedList<>(); q.add(new position(0,0)); boolean[][] visited = new boolean[h][w]; visited[0][0] = true; position p; while (!q.isEmpty()) { p = q.poll(); int x = p.x; int y = p.y; for(int i=0; i<4; i++) { int next_x = x + nx[i]; int next_y = y + ny[i]; if (0 <= next_x && next_x < h && 0 <= next_y && next_y < w){ if(visited[next_x][next_y] == false && maps[next_x][next_y] > 0) { visited[next_x][next_y] = true; maps[next_x][next_y] = maps[x][y] + 1; q.add(new position(next_x, next_y)); } } } } return maps[h-1][w-1] == 1 ? -1 : maps[h-1][w-1]; } }문제 풀이(Answer Code1)
-
최소의 길을 구하기 위해서는
BFS를 사용하는게 더 효율적이다.DFS는 깊게 탐색하는 탐색 알고리즘으로 잘못된 길을 탐색하다간 오히려 효율적이지 못할 수도 있다. -
반면에
BFS는 너비를 탐색하는 알고리즘으로 주변부터 탐색하기 때문에 DFS보다는 최소의 길을 찾을 수 있다. -
참고로,
DFS는 Stack, 재귀함수를 이용하여 구현하며, BFS는 Queue를 이용하여 구현한다. -
Queue는 데이터를 꺼낼 때마다 항상 첫 번째 지정된 데이터를 삭제하므로, 데이터의 추가/삭제가 쉬운LinkedList로 구현하는 것이 더 적합하다.
Answer Code2(23.11.08)
import java.util.*; class Solution { int[] dx = {-1, 1, 0, 0}; int[] dy = {0, 0, -1, 1}; public int solution(int[][] maps) { int answer = 0; // 행의 길이, 열의 길이 int[][] visited = new int[maps.length][maps[0].length]; visited[0][0] = 1; // 시작 위치 방문체크 // bfs 탐색 bfs(maps, visited); // 도착지 값을 넣어주기 // 배열의 인덱스는 0부터 시작하므로, 도착 위치(n-1, m-1)이 된다. answer = visited[maps.length -1][maps[0].length -1]; // 갈 수 없다면 -1 리턴 if (answer == 0) { answer = -1; } return answer; } public void bfs(int[][] maps, int[][] visited) { Queue<int[]> q = new LinkedList<>(); q.add(new int[]{0,0}); while(!q.isEmpty()) { int[] now = q.poll(); int x = now[0]; int y = now[1]; // 4방 탐색 for(int i = 0; i < 4; i++) { // 이동했을 때 위치 int nx = x + dx[i]; int ny = y + dy[i]; // 범위 벗어나는지 체크 // 방문했는지 체크 // 갈 수 있는 곳인지 체크 if(nx >= 0 && nx < maps.length && ny >= 0 && ny < maps[0].length && visited[nx][ny] == 0 && maps[nx][ny] == 1) { // 방문했다고 체크해주기 visited[nx][ny] = visited[x][y] + 1; // 큐에 넣기 q.add(new int[]{nx, ny}); } } } } }문제풀이 - Answer Code2
풀이 접근 방법
-
4방 탐색을 위한 dx, dy 배열을 만들어준다.
-
방문 체크를 위한 배열을 만들어준다.
-
시작 위치를 1로 만들어 방문 체크를 해준다.
-
bfs 탐색을 한다.
-
범위를 벗어나는지, 방문 했는지, 갈수 있는 곳인지를 체크한다.
-
체크해서 문제가 없다면 해당 위치까지 방문한 수 + 1을 넣어준다.
-
bfs를 추가적으로 탐색한다.
-
결과를 answer에 넣는다.
-
answer가 0이라면 도착할 수 없는 곳이므로 -1로 넣어준다.
-
결과를 출력한다.
-
visited[nx][ny] = visited[x][y] + 1;: 여기서nx,ny는 현재 위치에서 이동한 새로운 위치를 나타냅니다.visited[x][y]는 현재 위치까지의 이동 횟수를 나타내고, 여기에 1을 더해visited[nx][ny]에 저장한다. 이렇게 하면 새로운 위치까지의 이동 횟수가 기존 위치보다 1 더 많아지게 된다.예를 들어, 현재 위치에서
(nx, ny)로 이동했을 때, 이동 횟수가 3이었다면,visited[nx][ny]에는 4가 저장된다. -
q.add(new int[]{nx, ny});: 새로운 위치(nx, ny)를 큐에 추가합니다. 이렇게 하면 다음에 이 위치를 기준으로 탐색이 이어지게 된다.
이 두 단계를 통해, BFS 알고리즘이 현재 위치에서 갈 수 있는 모든 이동 가능한 위치를 탐색하고, 그 위치들을 큐에 추가하여 계속해서 탐색을 진행합니다. 이 과정을 통해 최단거리를 찾게 된다.
Review
-
BFS 개념은 알았지만 구현 방식에 있어서 알고리즘이 어떻게 짤지 구체적으로 떠오르지 못했다.
-
두번째로 할 때가 첫번째보다 이해가 더 쉬웠다.
-
다음에는 바로 생각날 수 있도록 + 접근 방식대로 풀어보도록 하자!
23.12.04
-
항상 dfs로만 풀어왔어서 bfs로 푸는 방법이 기억이 나질 않아, 결국 이전 풀이를 참고하게 되었다.
-
해당 풀이 방식보다 조금 더 나은게 있을 거 같은데, 생각나면 업데이트를 해보자!
Reference
- https://blackvill.tistory.com/177 - Answer Code2
-
[JPA] 값 타입
이 글은 [자바 ORM 표준 JPA 프로그래밍 - 기본편] 강의를 듣고 정리한 내용입니다.
기본값 타입
-
엔티티 타입
-
@Entity로 정의하는 객체이다. -
데이터가 변해도 식별자로 지속해서 추적이 가능하다.
-
ex) 회원 엔티티의 키나 나이 값을 변경해도 식별자로 인식이 가능하다.
-
-
값 타입
-
int, Integer, String 처럼 단순히 값으로 사용하는 자바 기본 타입이나 객체이다.
-
식별자가 없고 값만 있으므로 변경시 추적 불가능하다
-
ex) 게시판의 내용(content)
-
값 타입 분류
-
기본 값
-
자바 기본 타입(int, double)
-
래퍼 클래스(Integer, Long)
-
String
-
// 기본 값 타입 - 예시) - id, userName @Entity public class Member { @Id @GeneratedValue @Column(name = "member_id") private Long id; private String userName; }-
임베디드 타입(Embedded type, 복합 값 타입) - ex) 우편번호
-
컬렉션 값 타입(Collection value type)
임베디드 타입
-
임베디드 타입는 복합 값 타입으로 새로운 값 타입을 직접 정의할 수 있다. -
주로 기본 값 타입을 모아서 만들어 복합 값 타입이라고도 한다.
-
임베디드 타입 역시 직접 정의를 할 뿐, int, String과 같은 타입으로 이루어진다.
-
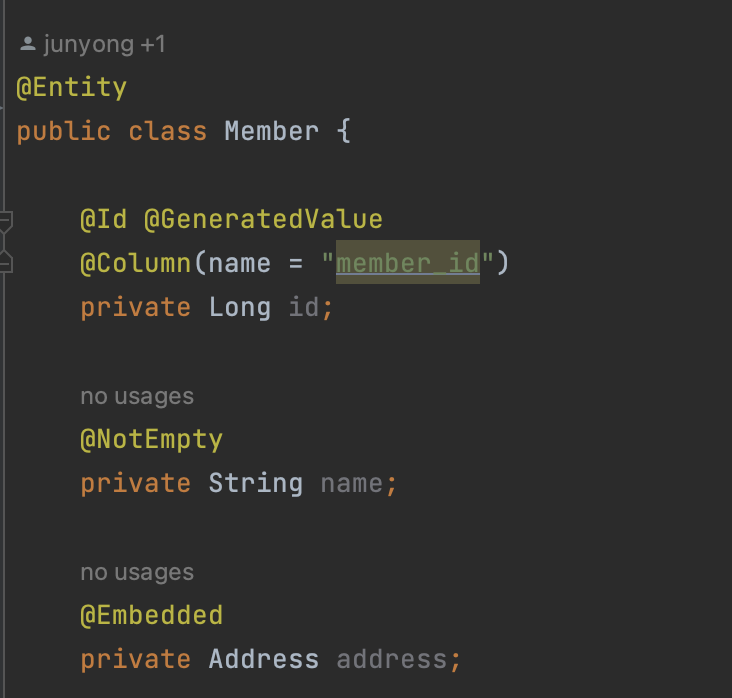
예를 들어, 회원 엔티티에 이름, 근무기간, 집 주소를 가질 때 -> 아래와 같이
Address클래스 임베디드 타입으로 바꿀 수 있다. -
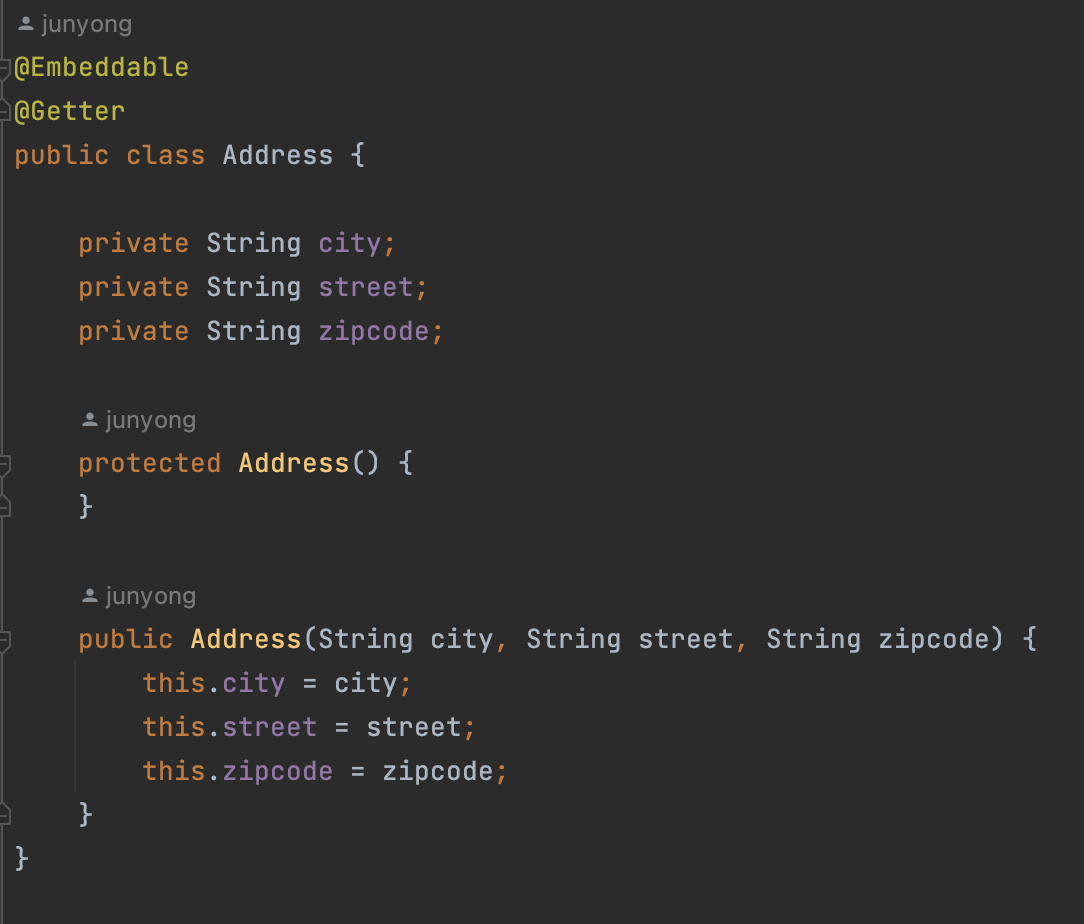
임베디드 타입을 사용하려면 값 타입을 정의하는 곳(Address)에 기본 생성자를 필수로 생성해야 한다.
임베디드 타입 사용법
-
@Embeddable: 값 타입을 정의하는 곳에 표시한다. -> Address 클래스 -
@Eembedded: 값 타입을 사용하는 곳에 표시한다. -> Member 클래스 안에 Address 객체를 필드로 선언한 뒤, 그 위에 표시해준다.
임베디드 타입의 장점
-
재사용성과 높은 응집도
-
임베디드 타입을 포함한 모든 값 타입은, 값 타임을 소유한 엔티티에 생명주기를 의존한다.
임베디드 타입과 테이블 매핑
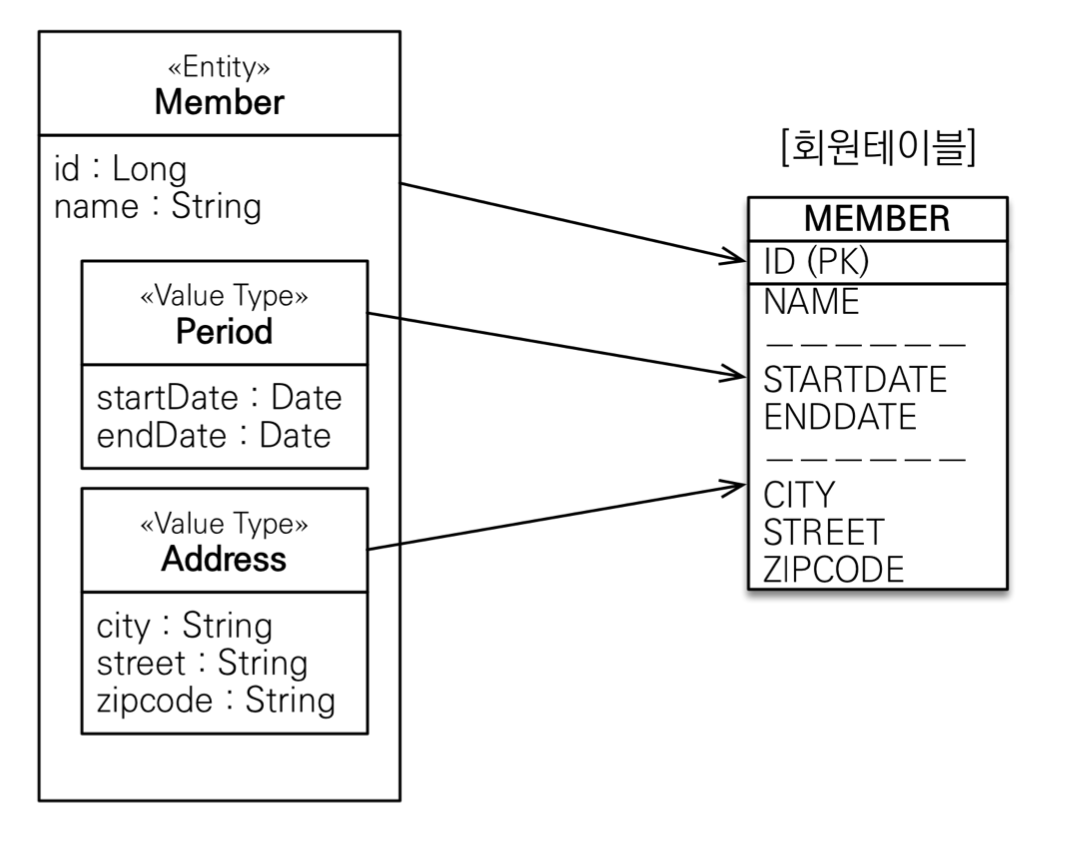
-
임베디드 타입은 엔티티의 값일 뿐이다. 그래서 임베디드 타입을 사용하기 전과 후에 매핑하는 테이블은 같다.
-
객체와 테이블을 아주 세밀하게 매핑하는 것이 가능하다.
-
잘 설계한 ORM 애플리케이션은 매핑한 테이블의 수보다 클래스의 수가 더 많다.
@AttributeOverride: 속성 재정의
-
한 엔티티에서 같은 값 타입을 사용하면 컬럼명이 중복될때,
@AttributeOverrides,@AttributeOverride를 사용해서 컬러명 속성을 재정의한다. -
아래 그림과 같이 주소라는 컬럼명을 재정의하기 위해
workAddress변수를 만들고, 그 위에@AttributeOverrides,@AttributeOverride을 사용했다.

값 타입과 불변 객체
-
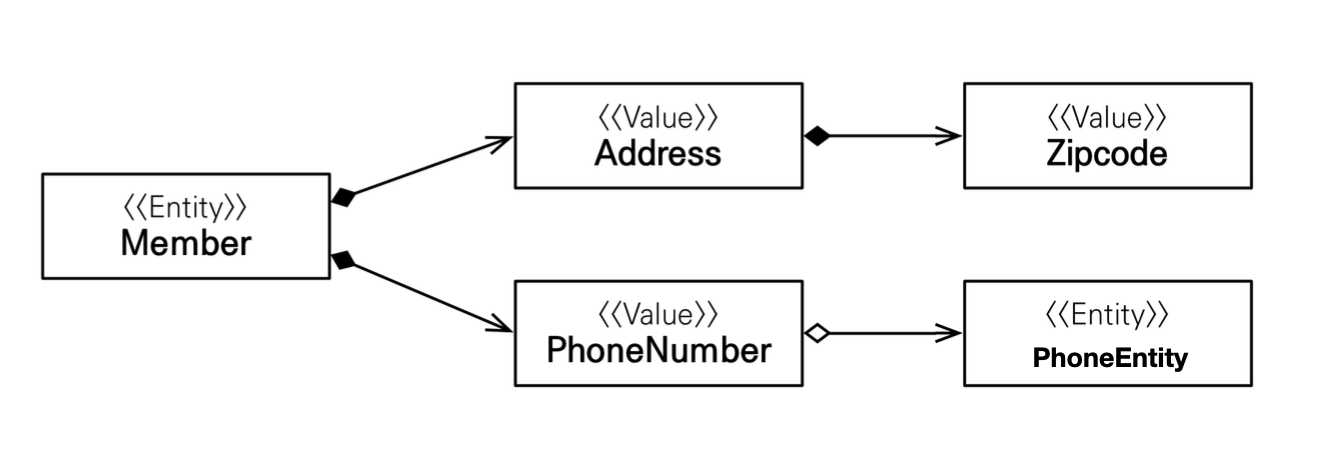
값 타입 공유 참조 - 임베디드 타입 같은 값 타입을 여러 엔티티에서 공유하면 위험함 → 부작용이 발생할 수 있다.
-
따라서 부작용을 피하기 위해서는 값 타입을 복사해준다.
-
값 타입의 실제 인스턴스인 값을 공유하는 것은 위험하다.
-
대신 값(인스턴스)를 복사해서 사용한다.
-
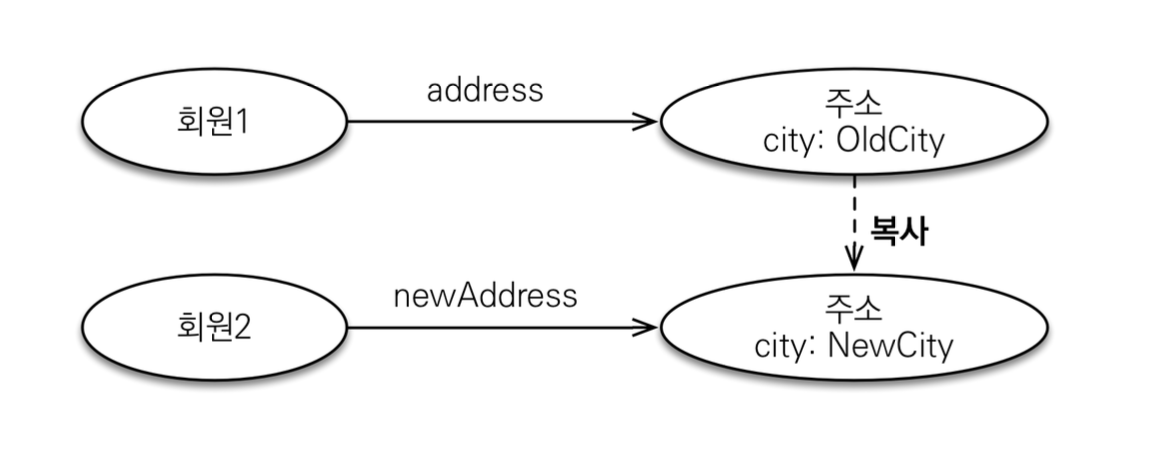
값 타입의 한계
-
항상 값을 복사해서 사용하면 공유 참조로 인해 발생하는 부작용을 피할 수 있지만, 문제는 임베디드 타입처럼 직접 정의한 값 타입은 자바의 기본 타입이 아니라
객체 타입이다. -
객체 타입을 수정할 수 없게 만들기 위해서는 값 타입을
불변 객체로 설계해야 한다.불변 객체: 생성 시점 이후에 절대 값을 변경할 수 없는 객체를 말한다.
-
불변 객체로 설계하기 위해서는 생성자로만 값을 설정하고, 수정자(Setter)를 만들지 않으면 된다.
-
참고로, Integer, String은 자바가 제공하는 대표적인 불변 객체이다.
-
불변이라는 작은 제약으로 부작용이라는 큰 재양을 막을 수 있다.
값 타입의 비교
-
값 타입을 비교할 때 동일성 비교(==) 보다는 동등성 비교(equals)을 이용하여 비교한다.
-
동일성(identity) 비교: 인스턴스의 참조 값을 비교해서,==을 사용한다. -
동등성(equivalence) 비교: 인스턴스의 값을 비교해서,equals()을 사용한다. -
동등성 비교(equals())을 사용하기 위해서는 해당 메서드를 적절하게 재정의 해줘야 한다.
-
해당 체크를 통해 필드에 직접 접근이 아닌 getter를 통해서 동등성을 비교하도록 한다. 그래야 프록시 객체에 접근할 수 있도록 하여 비교가 가능해진다.
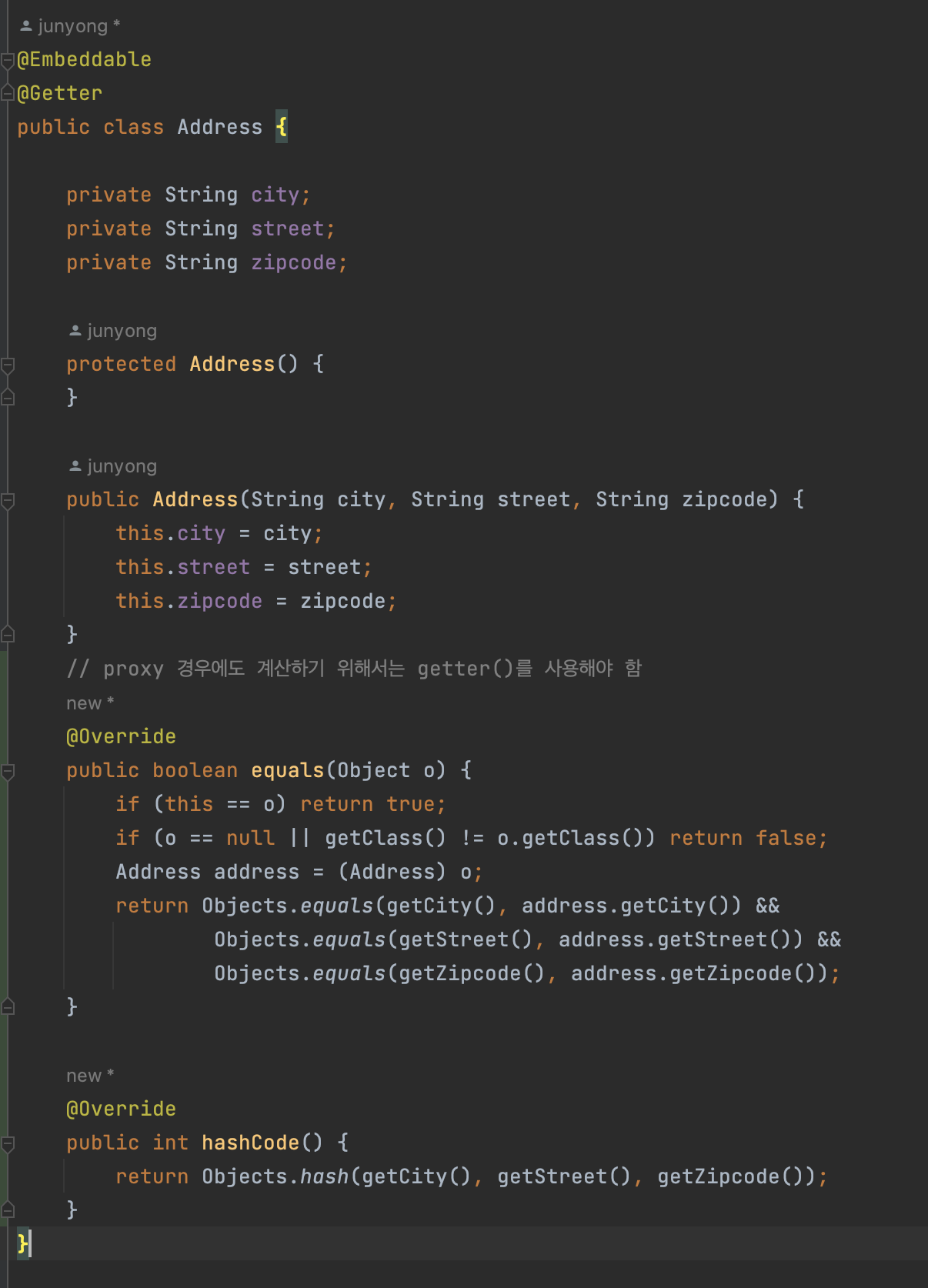

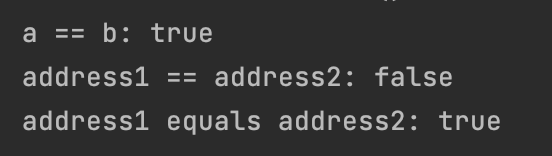
값 타입 컬렉션
-
값 타입을 하나 이상 저장할 때에는
값 타입 컬렉션을 사용한다. 그래서 컬렉션의 경우 1대다 관계로 되어있다. -
테이블로 보면 아래와 같이 favoriteFoods, addressHistory와 같이 되어있다.
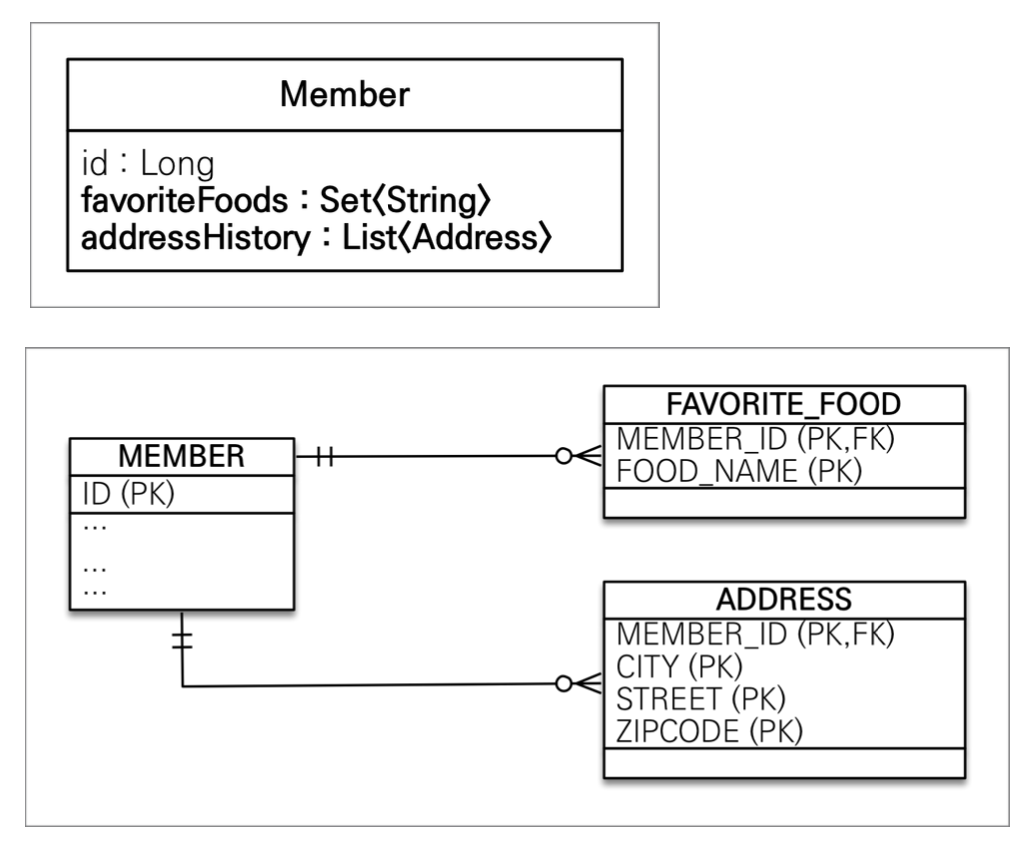
-
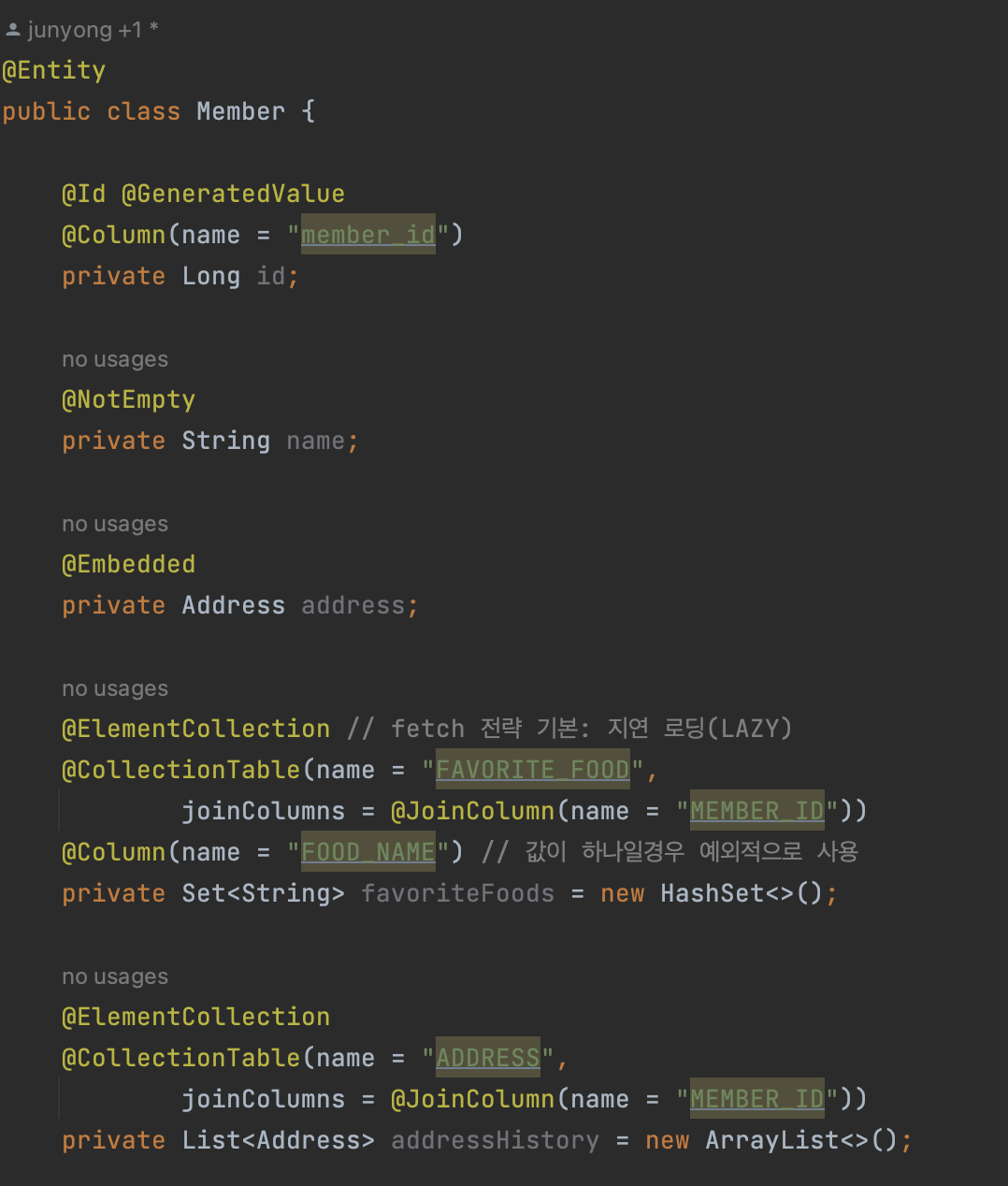
값 타입을 하나 이상 저장할 때,
@ElementCollection,@CollectionTable을 사용한다. -
@ElementCollection어노테이션을 사용하여 값 타입 컬렉션을 지정하고(fetch 전략 기본이 지연 로딩(LAZY)임),@CollectionTable어노테이션을 통해 값 타입 컬렉션이 사용할 테이블을 지정해준다.
값 타입 컬렉션의 제약사항
-
하지만 값 타입 컬렉션은 다음과 같은 제약사항이 있다.
-
값 타입은 엔티티와 다르게 식별자 개념이 없고, 값을 변경하면 추적이 어렵다.
-
값 타입 컬렉션에 변경 사항이 발생하면 주인 엔티티와 연관된 모든 데이터를 삭제하고, 값 타입 컬렉션에 있는 현재 값을 모두 저장하게 된다.
-
그리고 값 타입 컬렉션을 매핑하는 테이블은 모든 컬럼을 묶어서 기본 키를 구성해야 한다. -> null 입력X, 중복 저장X
-
-
따라서 값 타입 컬렉션을 사용하는 걸 추천하지는 않는다.
값 타입 컬렉션의 대안
-
대신, 값 타입 컬렉션의 대안으로 실무에서는 상황에 따라 값 타입 컬렉션 대신에 일대다 관계를 고려한다.
-
일대다 관계를 위한 엔티티를 만들고 여기에서 값 타입을 사용한다.
-
영속성 전이(Cascade) + 고아 객체 제거(orphan remove) 를 사용해서 값 타입 컬렉션 처럼 사용하는 방법이 있다. ⇒ ex)
AddressEntity -
아래와 같이 AddressEntity 라는 엔티티 테이블을 만들고, Member 테이블과 연관관계를 맺어준다.
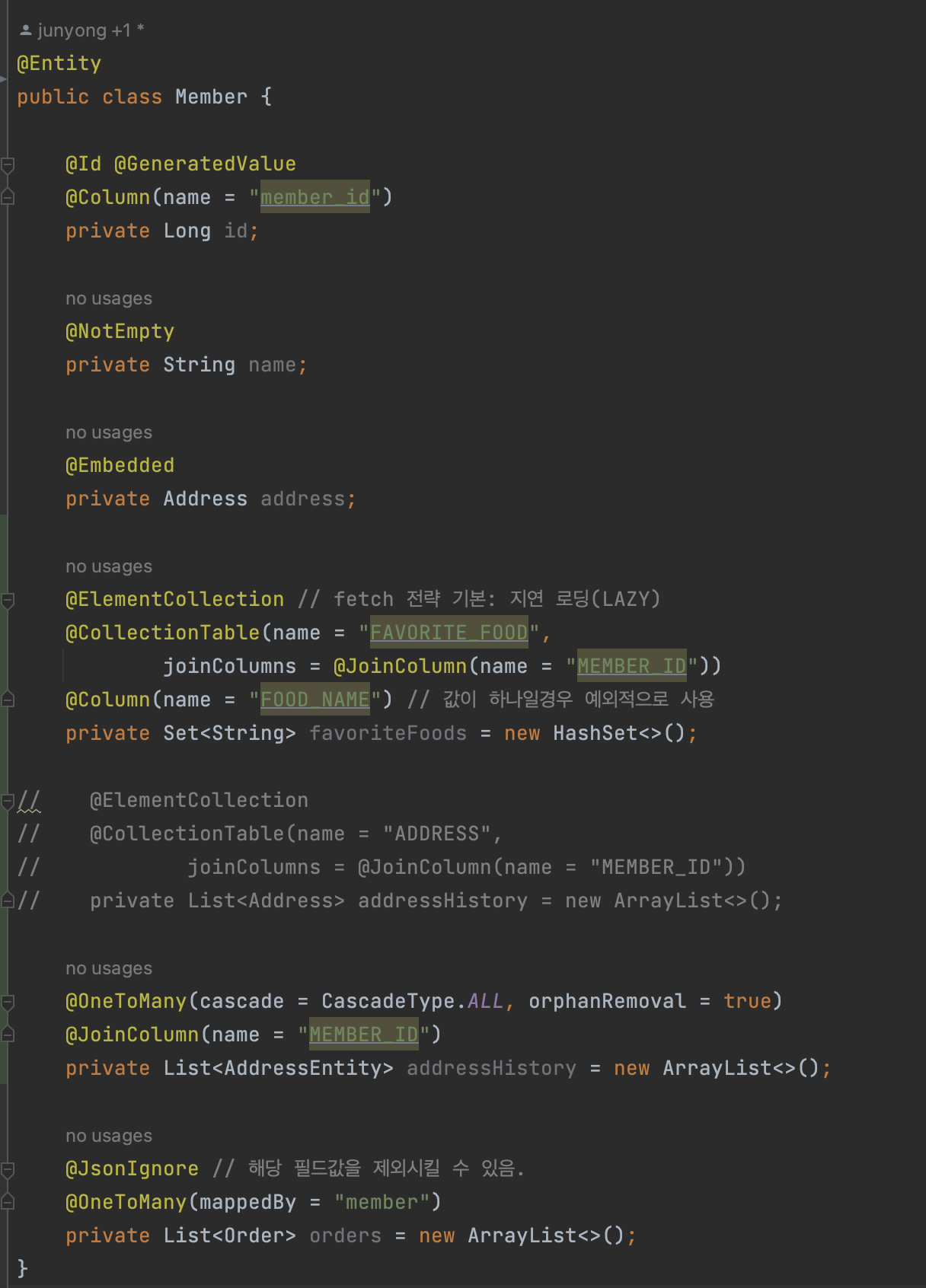
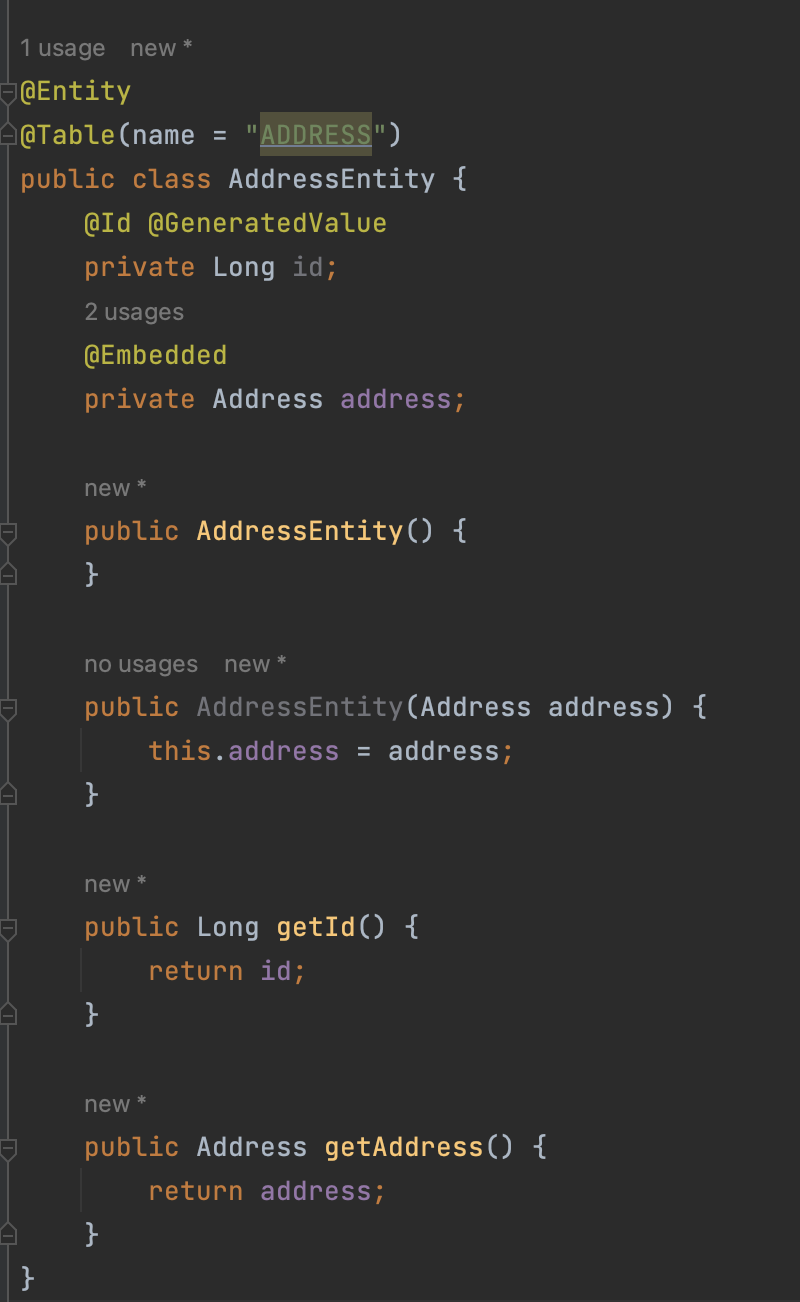
- 값 타입 컬렉션은 select box 처럼 멀티로 체크하는 등 단순한 경우에만 사용하는 것을 권장한다.
엔티티 타입과 값 타입의 특징
-
엔티티 타입의 경우 식별자가 있고, 생명 주기를 관리하며, 공유가 된다.
-
값 타입의 경우 식별자가 없고, 생명 주기를 엔티티에 의존하고 공유하지 않는 것이 안전하다. -> 복사해서 사용하거나 불변 객체로 만드는 것이 안전하다.
=> 정리하면, 식별자가 필요하고, 지속해서 값을 추적, 변경해야 한다면 그것은 값 타입이 아닌
엔티티를 사용하는 걸 권장한다.Reference
-
- DevHistory 4
- Essay 1
- Java 10
- Spring 15
- SpringBoot 17
- JPA 13
- MySQL 3
- Flyway 1
- Kafka 8
- Technology 22
- GoodCode 7
- Side_Project 20
- Retrospective 4
- AlgorithmSkill 3
- LeetCode 2
- Algorithm 70
- SQL 9
- OS 14
- Database 8
- Network 7
- HTTP 7
- DataStructure 5
- Linux 4
- Woowacourse 4
- Git 9
- AssertJ 1
- IntelliJ 5
- Probability-Statistics 5
- Electronic-Finance 13
- Business-Statistics 13
- Competition 1
- Book 6
- Workout 7
- E.T.C 8