지금의 기록이 미래의 자산이 된다.

Today's records become tomorrow's assets.

equals와 hashCode 관계

2023-12-06

devFancy

Java
이 글은 자바의 정석 책에서 나온 개념과 예제를 학습하고 정리한 글입니다.

java.lang 패키지
- java.lang 패키지는 자바프로그래밍에서 가장 기본이 되는 클래스를 포함하고 있다.
- 그렇기 때문에 java.lang 패키지의 클래스들은 import문 없이도 사용할 수 있게 되어 있다.
  - java.lang 패키지에 포함되는 클래스 : Object, String, StringBuffer, StringBuilder, Math, Wrapper
- java.lang 패키지의 여러 클래스들 중에서 자주 사용되는 Object 클래스와 관련 메서드에 대해 학습해보자.
Object 클래스
- Object 클래스는 모든 클래스의 최고 조상이기 때문에 Object 클래스의 멤버들은 모든 클래스에서 바로 사용 가능하다.
- Object 클래스는 멤버변수는 없고 오직 11개의 메서드만 가지고 있다. 이 메서드들은 모든 인스턴스가 가져야 할 기본적인 것들이며, 이 중에서 중요한 몇 가지만 살펴보자.
  
  (11개 메서드에 대해 확인하고 싶으면, “자바의 정석” p.450을 참고하자)
equals(Object obj)
- equals()는 매개변수로 객체의 참조변수를 받아서 비교하여 그 결과를 boolean 값으로 알려주는 역할을 한다.
- 아래의 코드는 Object 클래스에 정의되어 있는 equals의 실제 내용이다.
```
public boolean equals(Object obj){
        return(this == obj);
}
```
- 두 객체의 같고 다름을 참조변수의 값으로 판단한다. 그렇기 때문에 서로 다른 두 객체를 equals 메서드로 비교하면 항상 false를 결과로 얻게 된다.
  
  equals 메서드는 주소값으로 비교하기 때문에, 멤버변수의 값이 서로 같을지라도 참조변수의 값(주소값)이 다르면 false일 수 밖에 없다.
- Object 클래스로부터 상속받은 equals 메서드는 결국 두개의 참조변수가 같은 객체를 참조하고 있는지, 즉 두 참조변수에 저장된 값(주소값)이 같은지를 판단하는 기능밖에 할 수 없다는 것을 알 수 있다.
  
  equals 메서드로 인스턴스가 가지고 있는 value 값을 비교하도록 할 수 있는 방법은 equals 메서드를 오버라이딩하여 주소가 아닌 객체에 저장된 내용을 비교하도록 변경하면 된다.
```
class Person {
    long id;
    
    @Override
    public boolean equals(Object obj) {
        if(obj instanceof Person) {
            return id == ((Person) obj.id); // obj가 Object 타입이므로 id 값을 참조하기 위해서는 Person 타입으로 형변환이 필요하다.
        } else
            return false; // 타입이 Person이 아니면 값을 비교할 필요도 없다.
    }
    
    Person(long id) {
        this.id = id;
    }
}

class EqualsEx {
  public static void main(String[] args) {
      Person p1 = new Person(12345L);
      Person p2 = new Person(12345L);
      
      if(p1 == p2)
          System.out.println("p1과 p2는 같은 사람입니다.");
      else 
          System.out.printf("p1과 p2는 다른 사람입니다."); // 첫번째 결과
      
      if(p1.equals(p2)) 
          System.out.println("p1과 p2는 같은 사람입니다."); // 두번째 결과
      else 
          System.out.printf("p1과 p2는 다른 사람입니다.");
  }
}
```
- equals 메서드가 Person 인스턴스의 주소값이 아닌 멤버변수 id의 값을 비교하도록 하기 위해 equals 메서드를 다음과 같이 오버라이딩했다.
  
  이렇게 함으로써 서로 다른 인스턴스일지라도 같은 id(주민등록번호)를 가지고 있다면, equals 메서드로 비교했을 때, true로 결과를 얻게 할 수 있다.
- String 클래스 역시 Obejct 클래스의 equals 메서드를 그대로 사용하는 것이 아니라 이처럼 오버라이딩을 통해서 String 인스턴스가 갖는 문자열 값을 비교하도록 되어있다.
  
  그렇기 때문에 같은 내용의 문자열을 갖는 두 String 인스턴스에 equals 메서드를 사용하면 항상 true 값을 얻을 수 있다.
hashCode()
- hashCode 메서드는 해싱(hashing)기법에 사용되는 ‘해시함수(hash function)’을 구현한 것이다.
  
  해싱은 데이터관리기법 중 하나인데 다량의 데이터를 저장하고 검색하는데 유용하다.
- 해시함수는 찾고자 하는 값을 입력하면, 그 값이 저장된 위치를 알려주는 해시코드(hashcode)를 반환한다.
  
  일반적으로 해시코드가 같은 두 객체가 존재하는 것은 가능하지만, Object 클래스에 정의된 hashCode 메서드는 객체의 주소값을 int 값으로 해시코드를 만들어 반환하기 때문에 32 bit JVM에서는 서로 다른 두 객체는 결코 같은 해시코드를 가질 수 없었다.
  
  하지만 64 bit JVM에서는 8 byte 주소값으로 해시코드(4 byte)를 만들 수 있기 때문에 해시코드가 중복될 수 있다.
- 앞서 살펴본 것과 같이 클래스의 인스턴스 변수 값으로 객체의 같고 다름을 판단해야 하는 경우라면 equals 메서드 뿐 만 아니라 hashCode 메서드도 적절히 오버라이딩해야 한다.
  
  같은 객체라면 hashCode 메서드를 호출했을 때의 결과값인 해시코드도 같아야 하기 때문이다.
```
class HashCodeEx {
  public static void main(String[] args) { 
      String str1 = new String("hello");
      String str2 = new String("hello");

      System.out.println(str1.hashCode()); // 12345
      System.out.println(str2.hashCode()); // 12345
  }
}
```
- String 클래스는 문자열의 내용이 같으면, 동일한 해시코드를 반환하도록 hashCode 메서드가 오버라이딩되어 있기 때문에, 문자열 내용이 같은 str1과 str2에 대해 hashCode()를 호출하면 항상 동일한 해시코드값을 얻는다.
  
  반면에 Object 클래스의 hashCode 메서드처럼 객체의 주소값으로 해시코드를 생성하기 때문에 모든 객체에 대해 항상 다른 해시코드값을 반환할 것을 보장한다.
참고: 해싱기법을 사용하는 HashMap이나 HashSet과 같은 클래스에 저장할 객체라면 반드시 hashCode 메서드를 오버라이딩 해야한다. - 자바의 정석 11장. 컬렉션 프레임웍 -

equals와 hashCode를 같이 재정의 해야하는 이유

equals만 재정의할 경우

우선 예제로 사용될 Product 클래스를 살펴보자.
```
public class Product {
    private final String name;

    public Product(String name) {
        this.name = name;
    }

    // intellij Generate 기능 사용
    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
        Product product = (Product) o;
        return Objects.equals(name, product.name);
    }
}
```
- Product 클래스에는 equals만 재정의했다.
```
public static void main(String[] args){
    Product product1 = new Product("아메리카노");
    Product product2 = new Product("아메리카노");
    
    // true 출력
    System.out.println(product1.equals(product2));
}
```
- equals를 재정의했기 때문에 Product 객체의 name이 같은 product1, product2 객체는 논리적으로 같은 객체로 판단된다.
- 이제 아래 main 메서드의 출력 결과를 예측해보자.
```
public static void main(String[] args) {
    List<Product> products = new ArrayList<>();
        products.add(new Product("아메리카노"));
        products.add(new Product("아메리카노"));

    System.out.println(products.size());
}
```
- Product 객체를 2개 List<Product> products에 넣어줬으니 출력 결과는 당연히 2일 것이다.
- 그렇다면 이번엔 Collection에 중복되지 않는 Product 객체만 넣으라는 요구사항이 추가되었다고 가정해보자.
- 요구사항을 반영하기 위해 List에서 중복 값을 허용하지 않는 Set으로 로직을 바꿨다.
```
public static void main(String[] args) {
    Set<Product> products = new HashSet<>();
        products.add(new Product("아메리카노"));
        products.add(new Product("아메리카노"));

    System.out.println(products.size());
}
```
- 추가된 두 Product 객체의 이름이 같아서 논리적으로 같은 객체라 판단하고 HashSet의 size가 1이 나올거라 예상했지만, 예상과 다르게 2가 출력된다.
- hashCode를 equals와 함께 재정의하지 않으면 코드가 예상과 다르게 동작하는 위와 같은 문제를 일으킨다.
- 정확히 말하면 hash 값을 사용하는 Collection(HashSet, HashMap, HashTable)을 사용할 때 문제가 발생한다.
문제가 발생하는 이유
- hash 값을 사용하는 Collction(HashMap, HashSet)은 객체가 논리적으로 같은지 비교할 때 아래 그림과 같은 과정을 거친다.
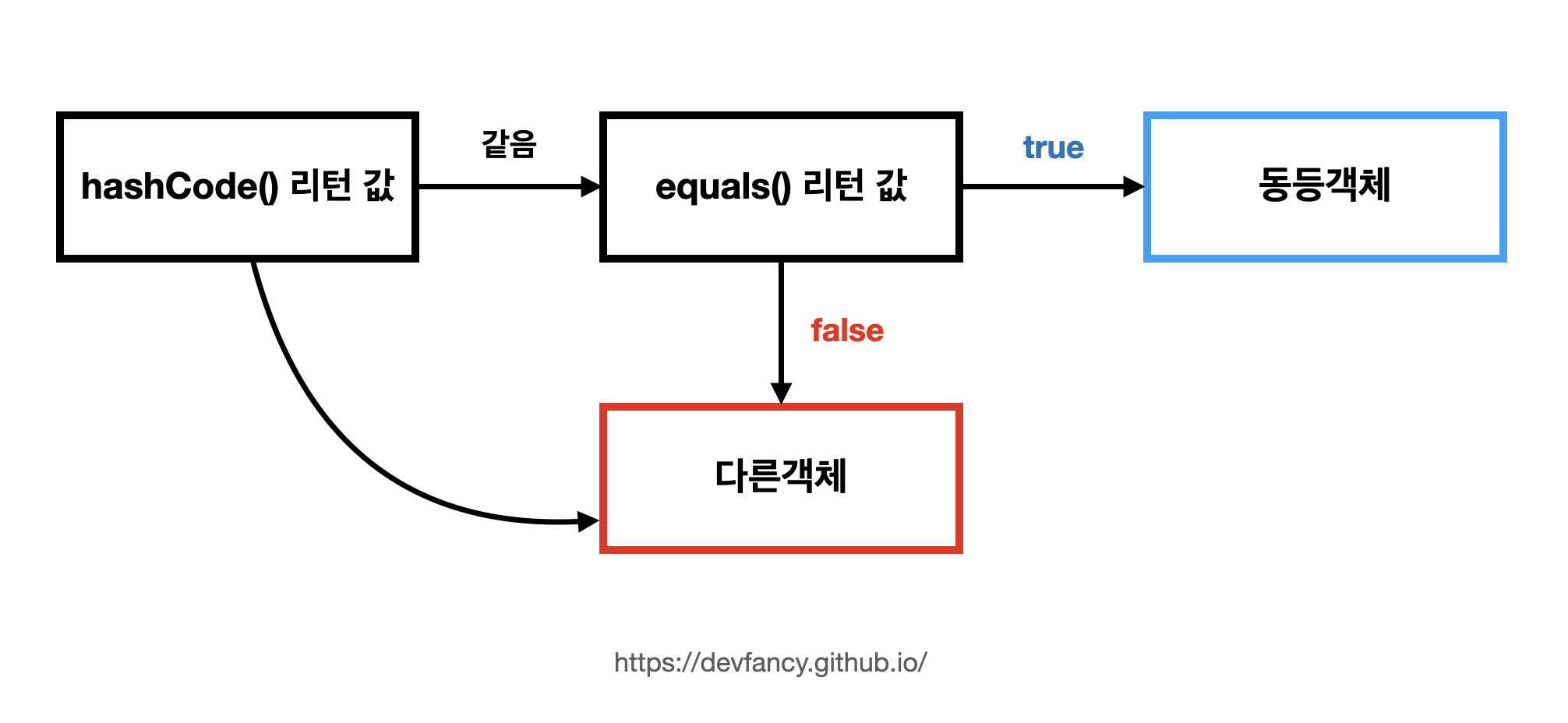
- [1] hashCode 메서드의 리턴 값이 우선 일치하고 [2] equals 메서드의 리턴 값이 true여야 논리적으로 같은 객체라고 판단한다.
- 앞서 봤던 main 메서드의 HashSet에 Product 객체를 추가할 때도 위와 같은 과정으로 중복 여부를 판단하고 HashSet에 추가됐다.
  
  다만 Product 클래스에는 hashCode 메서드가 재정의 되어있지 않아서 Object 클래스의 hashCode 메서드가 사용되었다.
  
  Object 클래스의 hashCode 메서드는 객체의 고유한 주소 값을 int 값으로 변환하기 때문에 객체마다 다른 값을 리턴한다.
  
  두 개의 Product 객체는 equals로 비교도 하기 전에 서로 다른 hashCode 메서드의 리턴 값으로 인해 다른 객체로 판단된 것이다.
해결방안: hashCode 오버라이딩
- 앞서 살펴봤던 문제를 해결하기 위해 Product 클래스에 hashCode 메서드를 아래와 같이 재정의했다.
```
public class Product {
    private final String name;

    public Product(String name) {
        this.name = name;
    }

    // intellij Generate 기능 사용
    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
      Product product = (Product) o;
        return Objects.equals(name, product.name);
    }

    @Override
    public int hashCode() {
        return Objects.hash(name);
    }
}
```
- intellij 의 Generate 기능을 사용했더니 Objects.hash 메서드를 호출하는 로직으로 hashCode 메서드가 재정의 됐다.
  
  Objects.hash 메서드는 hashCode 메서드를 재정의하기 위해 간편히 사용할 수 있는 메서드이지만 속도가 느리다.
  
  인자를 담기 위한 배열이 만들어지고 인자 중 기본 타입이 있다면 박싱과 언박싱도 거쳐야 하기 때문이다.
- 성능에 아주 민감하지 않은 대부분의 프로그램은 간편하게 Objects.hash 메서드를 사용해서 hashCode 메서드를 재정의해도 문제 없다.
  
  민감한 경우에는 직접 재정의해주는 게 좋다. (관련 정보 - Guide to hashCode() in Java)
무조건 재정의해야 할까?
- ‘hash 값을 사용하는 Collection을 사용하지 않는다면, equals와 hashCode를 같이 재정의(오버라이딩)하지 않아도 되는건가?’ 라고 생각할 수 있다.
- 사용자정의 클래스를 작성할 때 equals 메서드를 오버라이딩해야 한다면, hashCode()도 클래스의 작성의도에 맞게 재정의하는 것이 원칙이지만, 요구사항에 따라 할지 말지 결정하면 된다.
  
  (만약 Collection을 사용한다면 재정의 해주는게 맞다고 생각한다)
Reference
- 자바의 정석 - 9장. java.lang 패키지와 유용한 클래스 / 11장. 컬렉션 프레임웍
- Java 공식문서: HashMap
- Tecoble: equals와 hashCode는 왜 같이 재정의해야 할까?
Read All
[백준] 4963. 섬의 개수

2023-12-05

devFancy

Algorithm
문제 링크

성능 요약
- 메모리: 16012 KB, 시간: 176 ms
구분
- 그래프 이론, 그래프 탐색, 트리, 너비 우선 탐색, 깊이 우선 탐색
Answer Code

```java // 섬의 개수([백준] 4963.) - 23.12.04 import java.io.BufferedReader; import java.io.BufferedWriter; import java.io.IOException; import java.io.InputStreamReader; import java.io.OutputStreamWriter; import java.util.StringTokenizer;

public class Number_of_Islands { static final int MAX = 50 + 10; static boolean[][] map; static boolean[][] visited; static int M, N; static int[] dirY = {-1, -1, 0, 1, 1, 1, 0, -1}; // 상하좌우, 대각선 포함 - 8개 방향 static int[] dirX = {0, 1, 1, 1, 0, -1, -1, -1};

public static void dfs(int y, int x) { visited[y][x] = true; for(int i = 0; i < 8; i++) { int newY = y + dirY[i]; int newX = x + dirX[i]; if(map[newY][newX] && visited[newY][newX] == false) { dfs(newY, newX); } }

}

public static void main(String[] args) throws IOException { // 0. 입력 및 초기화 BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
Read All
[백준] 1388. 바닥장식

2023-12-05

devFancy

Algorithm
문제 링크

성능 요약
- 메모리: 14196 KB, 시간: 128 ms
구분
- 깊이 우선 탐색, 그래프 이론, 그래프 탐색, 구현
Answer Code1(23.12.05)

```java // 바닥장식([백준] 4963.) import java.util.; import java.io.;

class FloorDecoration { static final int MAX = 50 + 10; static char[][] map; static boolean[][] visited;

public static void dfs(int y, int x) { visited[y][x] = true;
```
if(map[y][x] == '-' && map[y][x+1] == '-') {
  dfs(y, x+1);
}
if(map[y][x] == '|' && map[y+1][x] == '|') {
  dfs(y+1, x);
}
```
} public static void main(String[] args) throws IOException { // 0. 입력 및 초기화 BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
```
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());

map = new char[MAX][MAX];
visited = new boolean[MAX][MAX];
```
Read All

[solved.ac] Class3++ 1012. 유기농 배추

2023-12-04

devfancy

Algorithm

성능 요약
구분
Answer Code1(2023.02.09) - BFS
Answer Code2(2023.02.09) - DFS

문제 링크

성능 요약

메모리: 16044 KB, 시간: 164 ms - Answer Code2(2023.02.09) - BFS
메모리: 16236 KB, 시간: 160 ms - Answer Code1(2023.02.09) - DFS
메모리: 15792 KB, 시간: 164 ms - Answer Code3(2023.12.04) - DFS

구분

그래프 이론(graphs), 그래프 탐색(graph_traversal), 너비 우선 탐색(bfs), 깊이 우선 탐색(dfs)

Answer Code1(2023.02.09) - BFS

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {

    static int[][] ground;      //2차원 배열로 배추밭을 표현한다
    static boolean[][] check;   //2차원 배열로 배추가 있는 곳을 체크한다
    static int weight;          //배추밭의 가로
    static int height;          //배추밭의 세로

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());
        StringTokenizer st;
        for (int i = 0; i < T; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            weight = Integer.parseInt(st.nextToken());
            height = Integer.parseInt(st.nextToken());
            ground = new int[weight][height];
            check = new boolean[weight][height];

            int K = Integer.parseInt(st.nextToken());
            for (int j = 0; j < K; j++) {
                st = new StringTokenizer(br.readLine(), " ");
                int x = Integer.parseInt(st.nextToken());
                int y = Integer.parseInt(st.nextToken());
                ground[x][y] = 1;   //배추 좌표 입력
            }
            //===========================================================
            //여기까지는 입력된 내용 저장하는 내용이다.

            int count=0;    //테스트 케이스마다 지렁이의 개수를 세야한다
            
            //bfs의 시작좌표를 셋팅해서 다른 곳에 모여있는 배추들도 파악할 수 있게한다
            //가로 세로 좌표들을 하나씩 입력해주고
            for (int j = 0; j < weight; j++) {
                for (int k = 0; k < height; k++) {
                    
                    //좌표에 배추가 있는지 확인, 내가 체크안한 곳인지 확인한다
                     if(ground[j][k] == 1 && !check[j][k]){
                         //배추가 있고 체크안된 좌표에서부터 bfs로 연결된 곳을 파악한다
                         bfs(j, k);
                         
                         //지렁이의 개수는 인접한 곳마다 1개씩이다.
                         //인접한 곳을 모두 파악했으면 지렁이를 한마리 놓는다.
                         count++;
                     }
                }
            }

            System.out.println(count);
        }

    }

    private static void bfs(int startX, int startY) {
        Queue<int[]> queue = new LinkedList<>();
        //bfs에서 queue의 역할은 다음 탐색할 좌표를 미리 저장해 놓는 것이다.
        //bfs 1번 실행될때마다 인접한 곳을 모두 탐색하고 종료되니 bfs안에 queue를 선언했다.
        
        queue.offer(new int[] {startX, startY});
        //x, y좌표 저장
        
        check[startX][startY] = true;
        //시작좌표엔 배추가 있으니 미리 true로 처리해준다.
        
        int[] X = {0, 0, -1, +1};
        int[] Y = {-1, +1, 0, 0};
        //배추가 상하좌우에 인접하면 이동할 수 있다.
        //현재좌표에서 상하좌우 움직이는 좌표를 지정한다.

        //queue가 비어있으면 더이상 인접한 배추가 없다는 뜻이다.
        while(!queue.isEmpty()){
            int[] poll = queue.poll();
            //저장된 queue를 꺼낸다
            
            //상하좌우 4가지 방법이니 for문 4번 반복
            for (int i = 0; i < 4; i++) {
                int x = poll[0] + X[i];
                int y = poll[1] + Y[i];
                //상하좌우 좌표 조정

                //좌표가 배추밭을 벗어나게되면 다음 좌표를 체크해야한다
                if(x < 0 || x >= weight || y < 0 || y >= height){
                    continue;
                }

                //상하좌우 움직인 좌표에 배추가 있고, 체크하지 않은 좌표이면
                if(ground[x][y] == 1 & !check[x][y]){
                    queue.offer(new int[] {x, y});
                    //좌표를 저장한다.
                    check[x][y] = true;
                    //체크한다
                }

            }
        }

    }

}

Answer Code2(2023.02.09) - DFS

```java import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.LinkedList; import java.util.Queue; import java.util.StringTokenizer;

public class Main {

static int[][] ground;      //2차원 배열로 배추밭을 표현한다
static boolean[][] check;   //2차원 배열로 배추가 있는 곳을 체크한다
static int weight;          //배추밭의 가로
static int height;          //배추밭의 세로

public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    int T = Integer.parseInt(br.readLine());
    StringTokenizer st;
    for (int i = 0; i < T; i++) {
        st = new StringTokenizer(br.readLine(), " ");
        weight = Integer.parseInt(st.nextToken());
        height = Integer.parseInt(st.nextToken());
        ground = new int[weight][height];
        check = new boolean[weight][height];

        int K = Integer.parseInt(st.nextToken());
        for (int j = 0; j < K; j++) {
            st = new StringTokenizer(br.readLine(), " ");
            int x = Integer.parseInt(st.nextToken());
            int y = Integer.parseInt(st.nextToken());
            ground[x][y] = 1;   //배추 좌표 입력
        }
        //===========================================================
        //여기까지는 입력된 내용 저장하는 내용이다.

        int count=0;    //테스트 케이스마다 지렁이의 개수를 세야한다

        //bfs의 시작좌표를 셋팅해서 다른 곳에 모여있는 배추들도 파악할 수 있게한다
        //가로 세로 좌표들을 하나씩 입력해주고
        for (int j = 0; j < weight; j++) {
            for (int k = 0; k < height; k++) {

                //좌표에 배추가 있는지 확인, 내가 체크안한 곳인지 확인한다
                 if(ground[j][k] == 1 && !check[j][k]){
                     //배추가 있고 체크안된 좌표에서부터 dfs로 연결된 곳을 파악한다
                     dfs(j, k);

                     //지렁이의 개수는 인접한 곳마다 1개씩이다.
                     //인접한 곳을 모두 파악했으면 지렁이를 한마리 놓는다.
                     count++;
                 }
            }
        }

        System.out.println(count);
    }

}

private static void dfs(int startX, int startY) {
    check[startX][startY] = true;
    //시작좌표엔 배추가 있으니 미리 true로 처리해준다.

    int[] X = {0, 0, -1, +1};
    int[] Y = {-1, +1, 0, 0};
    //배추가 상하좌우에 인접하면 이동할 수 있다.
    //현재좌표에서 상하좌우 움직이는 좌표를 지정한다.

    //상하좌우 4가지 방법이니 for문 4번 반복
    for (int i = 0; i < 4; i++) {
        int x = startX + X[i];
        int y = startY + Y[i];
        //상하좌우 좌표 조정

        //좌표가 배추밭을 벗어나게되면 다음 좌표를 체크해야한다
        if(x < 0 || x >= weight || y < 0 || y >= height){
            continue;
        }

        //상하좌우 움직인 좌표에 배추가 있고, 체크하지 않은 좌표이면
        if(ground[x][y] == 1 & !check[x][y]){
            dfs(x, y);	//해당 좌표로 dfs 실행
        }

    }

Read All

[백준] 13565. 침투

2023-12-04

devFancy

Algorithm

성능 요약
구분
Answer Code1(23.12.04)
- 문제풀이
Answer Code2(24.01.16)
정리
Review

문제 링크

성능 요약

메모리: 53320 KB, 시간: 1356 ms
메모리: 54268 KB, 시간: 696 ms

구분

그래프 이론, 그래프 탐색, 트리, 너비 우선 탐색, 깊이 우선 탐색

Answer Code1(23.12.04)

// 침투 (백준 13565)
import java.util.*;
import java.io.*;

class Penetrate {
  static final int MAX = 1000 + 10;
  static boolean[][] map;
  static boolean[][] visited;
  static int M, N;
  static int dirX[] = {-1, 1, 0, 0};
  static int dirY[] = {0, 0, -1, 1};
  static boolean answer;

  public static void dfs(int y, int x) {
    if(y == N) {
      answer = true;
      return;
    }

    visited[y][x] = true;
    for(int i = 0; i < 4; i++) {
      int newX = x + dirX[i];
      int newY = y + dirY[i];
      if(map[newY][newX] && visited[newY][newX] == false)
        dfs(newY, newX);
    }
  }

  public static void main(String[] args) throws IOException {
    // 0. 입력 및 초기화
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

    StringTokenizer st = new StringTokenizer(br.readLine());
    N = Integer.parseInt(st.nextToken());
    M = Integer.parseInt(st.nextToken());

    // 1. map에 정보 반영하기
    map = new boolean[MAX][MAX];
    visited = new boolean[MAX][MAX];

    for(int i = 1; i <= N; i++) {
      String str = br.readLine();
      for(int j = 1; j <= M; j++)
        map[i][j] = (str.charAt(j - 1) == '0' ? true : false);

    }

    // 2. dfs 수행
    for(int j = 1; j <= M; j++) {
      if(map[1][j]) {
        dfs(1, j);
      }
    }

    // 3. 출력
    if(answer) bw.write("YES");
    else bw.write("NO");

    bw.close();
    br.close();
  }
}

문제풀이

이 문제에서 DFS를 떠올릴 수 있는 키워드는 다음과 같다.
- 상하좌우로 인접한 흰색 격자들
- 안쪽까지 침두될 수 있는지 아닌지를 판단
문제에서는 전류가 흐르는 것을 ‘0’으로 해주고, 흐르지 않는 것을 ‘1’로 나와있는데, 이는 문제를 풀때 헷갈릴 수 있다.

그래서 전류가 흐르는 것을 ‘1’로 하고, 흐르지 않는 것을 ‘0’으로 해주기 위해 바꿔주는 로직을 구성한다.

이 문제에서 핵심은 내가 방문하고자 하는 곳을 1로 하는 것이 훨씬 더 유리하다.
이 문제에서는 첫 번째 줄에서 시작해서 마지막에 도달할 수 있는지 판단하는 것이므로 dfs(1, j)라고 해준 것이다.

[1]. map에 정보 반영하기

이중 반복문을 통해 해당 위치에 해당하는 값이 0일 경우, ‘1’로 바꿔준다.

[2]. dfs 수행

처음 시작 위치가 1부터 시작하기 때문에 dfs(1, j)과 같이 표현한 것이고,
M번 만큼 반복하면서 값이 true일 경우에 한해서만 dfs를 수행하기 때문에 for문 안에 조건문인 if(map[1][j])을 추가해준 것이다.
dfs를 수행할 때, 상하좌우로 확인하므로 반복문 for(int i = 0; i < 4; i++)과 방향에 대한 dirX, dirY를 선언해줬다.

그리고 상하좌우를 확인할 때, map에 해당하는 값이 true(1)이고, 방문한 적이 없을 경우에만 dfs를 다시 호출하도록 했다.
마지막으로 dfs 메서드 시작할 때, if(y == N)을 한 이유는 안쪽까지 도달했는지 확인하기 위해서다.

만약 안쪽까지 도달했다면, 즉 N번 줄에 도달했다면 침투를 했다는 의미이므로 answer 값을 true로 바꿔주고 return 해주면 된다.

[3]. 출력

출력할 때는 answer가 true이면 YES를 출력하고, 그게 아니라면 NO를 출력해주면 된다.

visited 없이 map으로만 구현하기

아래는 visited 없이 map으로도 구현한 코드이다.

import java.util.*;
import java.io.*;

class Penetrate {
    static final int MAX = 1000 + 10;
    static boolean[][] map;
    static int M, N;
    static int dirX[] = {-1, 1, 0, 0};
    static int dirY[] = {0, 0, -1, 1};
    static boolean answer;

    public static void dfs(int y, int x) {
        if(y == N) {
            answer = true;
            return;
        }

        map[y][x] = false;
        for(int i = 0; i < 4; i++) {
            int newX = x + dirX[i];
            int newY = y + dirY[i];
            if(map[newY][newX])
                dfs(newY, newX);
        }
    }

    public static void main(String[] args) throws IOException {
        // 0. 입력 및 초기화
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        map = new boolean[MAX][MAX];

        // 1. map에 정보 반영하기
        for(int i = 1; i <= N; i++) {
            String str = br.readLine();
            for(int j = 1; j <= M; j++) {
                map[i][j] = (str.charAt(j - 1) == '0' ? true : false);
            }
        }

        // 2. dfs 수행
        for(int j = 1; j <= M; j++) {
            if(map[1][j])
                dfs(1, j);
        }

        // 3. 출력
        if(answer) bw.write("YES");
        else bw.write("NO");

        bw.close();
        br.close();
    }
}

Answer Code2(24.01.16)

package DFS;
// 24.01.16 침투 복습
import java.util.*;
import java.io.*;

class Penetrate_2 {
    static final int MAX = 1000 + 10;
    static boolean[][] map;
    static int N, M;
    static boolean answer;

    static int[] dirX = {-1, 1, 0, 0};
    static int[] dirY = {0, 0, -1, 1};

    public static void dfs(int x, int y) {
        if(x == N) {
            answer = true;
            return;
        }
        map[x][y] = false;
        for(int i = 0; i < 4; i++) {
            int newX = x + dirX[i];
            int newY = y + dirY[i];
            if(map[newX][newY]) {
                dfs(newX, newY);
            }
        }

    }
    public static void main(String[] args) throws IOException {
        
        // 0. 입력 및 초기화
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        // 1. map에 정보반영
        map = new boolean[MAX][MAX];

        for(int i = 1; i <= N; i++) {
            String str = br.readLine();
            for(int j = 1; j <= M; j++) {
                map[i][j] = (str.charAt(j - 1) == '0' ? true : false);
            }
        }
        
        // 2. bfs 호출
        for(int j = 1; j <= M; j++) {
            if(map[1][j]) {
                dfs(1, j);
            }
        }

        // 3. 출력
        if(answer) bw.write("YES");
        else bw.write("NO");
        
        bw.close();
        br.close();
    }
}

정리

문제를 풀기 시작하기 전에, 아래 5가지를 생각해보면서 접근해보자.

상하좌우로 인접한 흰색 격자들로 전달 -> DFS/BFS
서로 연결되었다는 정보를 어떻게 하나의 자료구조로 통합할까? -> 2차원 배열
이미 방문한 지점을 다시 방문하지 않으려면 어떤 자료구조를 사용해야 할까?
visited 배열을 생략할 수는 없을까?
어느 지점에서 dfs를 시작할까?

Review

visited 없이 map으로만 할 경우 처리 시간이 1892(ms) -> 1356(ms) 줄었다는 걸 확인할 수 있다.
그래도 이해를 위해 우선 visited 변수를 사용해서 풀어보고, 완전히 dfs를 이해했다면 이후에는 visited 없이도 바로 생각할 수 있도록 하자.

Read All

16/64

지금의 기록이 미래의 자산이 된다.

equals와 hashCode 관계

java.lang 패키지

Object 클래스

equals(Object obj)

hashCode()

equals와 hashCode를 같이 재정의 해야하는 이유

equals만 재정의할 경우

문제가 발생하는 이유

해결방안: hashCode 오버라이딩

무조건 재정의해야 할까?

Reference

[백준] 4963. 섬의 개수

성능 요약

구분

Answer Code

[백준] 1388. 바닥장식

성능 요약

구분

Answer Code1(23.12.05)

[solved.ac] Class3++ 1012. 유기농 배추

성능 요약

구분

Answer Code1(2023.02.09) - BFS

Answer Code2(2023.02.09) - DFS

[백준] 13565. 침투

성능 요약

구분

Answer Code1(23.12.04)

문제풀이

Answer Code2(24.01.16)

정리

Review